"Investigating Properties of Kites". "Explorations for the Mathematics Classroom II" Using TI-92 GEOMETRY, Texas Instruments.
Charles Vonder Embse (Central Michigan University)
Arne Engebretsen (Grendale High School)
Charles Vonder Embse (Central Michigan University)
Arne Engebretsen (Grendale High School)
Un estel és un quadrilàter que cumpleix les condicions:
Té costats iguals dos a dos.
Els costats iguals són consecutius.
1. Construeix tu mateix un estel de diferents maneres que tens proposades a continuació.
Comprova que la construcció de baix és correcte. Mou tu mateix els punts lliures de les figures i comprova que la figura segueix essent un estel.
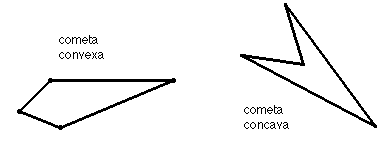
2. Observes dos tipus de figures diferents. Quin tipus de condició es compleix als estels convexos ?
3. Si unim els punts mitjos dels costats d'un estel. Quina mena de quadrilàter tenim ?
4. Dibuixa les diagonals d'un estel i observa si compleixen alguna propietat. Comprova també si aquesta propietat és observable als estels de forma còncava.
5. Dibuixa els casos particulars del quadrat i el rombe. Comprova si compleixen les propietats abans comentades i cerca també altres propietats que compleixen aquestes figures i que en canvi no compleixen els estels.
6. Sobre un full quadriculat, dibuixa un estel qualsevol i fes el càlcul de la seva àrea. Hi ha alguna relació entre l'àrea i les diagonals de l'estel ? Comprova la teva hipòtesi fent modificacions a la figura i observat que la propietat observada segueix essent vertadera.
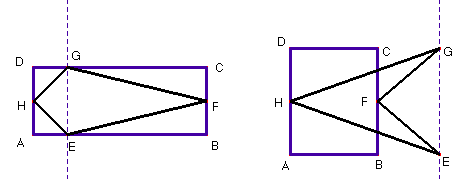
7. Inscriu a un rectangle ABCD un estel EFGH de manera que H i F siguin els punts mitjos dels costats AD i BC.
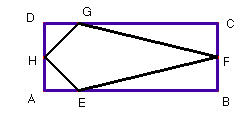
a) Hi ha alguna relació entre l'àrea de l'estel i la del rectangle ABCD ?
b) Com canvia aquesta relació a mesura que els punts E i G es mouen?
c) Quin és el valor màxim de l'àrea de l'estel ?
d) Observes alguna relació entre els perímetres de l'estel i el rectangle ?
e) Si el perímetre va canviant, quin és el seu valor mínim ?
SOLUCIONS.
1. CONSTRUIR ESTELS
Aquesta activitat es pot fer en grup per aportar més idees.
a) Dibuixar dos cercles que es tallin a dos punts. El quadrilàter que en resulta unint els punts de tall i els centres dels dos cercles és un estel.
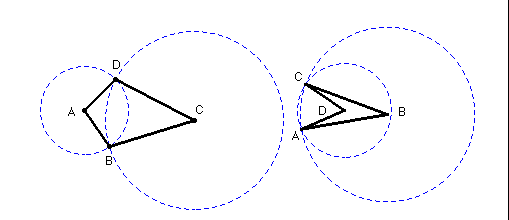
b) Dibuixar un segment AC i la seva mediatriu. Marcar dos punts B i D sobre la mediatriu. Juntem els punts ABCD. El quadrilàter que en resulta és un estel.
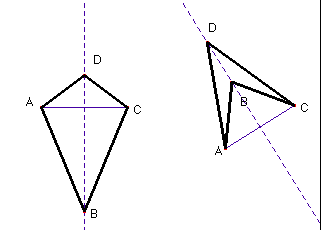
c) Dibuixa dos triangles isòsceles que tinguin la base comú. Els parells de costats iguals dels triangles donen un quadrilàter que és a la vegada un estel.
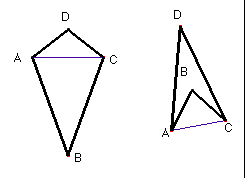
d) Dibuixa dos segments AD i AB que tinguin el punt comú A. Dibuixa la recta que uneix els altres extrems dels segments B i D. Fes una simetria axial dels segments agafant com a eix la recta que passa pels punts B i D. Els quatre segments resultants formen un estel.
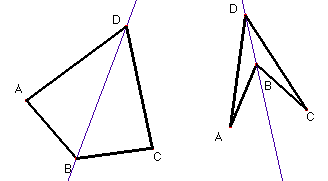
e) Dibuixa un rectangle qualsevol de vèrtexs ABCD. Marca els punts mitjos H i F de dos dels seus costats iguals. Dibuixa una recta paral·lela al costats anteriors que talli als altres o a les seves prolongacions en dos punts G i E. El polígon que en resulta ajuntant els punts HGFE és un estel correctament dibuixat.
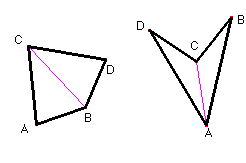
f) Dibuixa un triangle qualsevol de vèrtexs ABC. Fes el triangle simètric respecte l'eix de simetria format pel costat BC. Els vèrtexs ABC del triangle, juntament amb el vèrtex obtingut per simetria D, formen un estel.
2. Segons el mètode emprat per dibuixar l'estel. Aquest serà una figura còncava quan:
a) Els centres dels cercles es troben al mateix costat que els punts d'intersecció.
b) Els dos punts de la mediatriu es troben al mateix costat del segment.
c) Els vèrtexs B i D dels triangles es troben a un mateix costat del segment AC.
d) Quan els extrems no comuns C i A es troben al mateix costat de la recta perpendicular a l'eix de simetria.
e) Quan la recta paral·lela talla a les extensions dels costats.
f) Quan l'altura traçada sobre el costat que juga el paper d'eix de simetria no talla al costat sinó a una extensió.
3. El quadrilàter que en resulta desprès d'ajuntar els punts mitjos dels costats d'un estel és, en qualsevol dels casos, un rectangle.
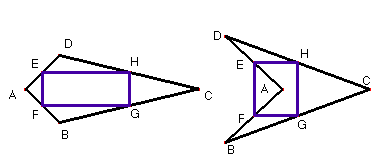
Dibuja cada diagonal de la cometa. Los segmentos medios de los triángulos formados por la diagonal de la cometa son paralelos a la base (diagonal) y por tanto paralelos a cada lado. Esta propiedad se cumple para las dos diagonales y los dos pares de segmentos paralelos.
Una de las formas con que hemos definido la cometa es como los lados de dos triángulos isósceles, que tienen en común la base. Si se utiliza esta definición, la diagonal que une el tercer vértice de uno de los triángulos con el del otro, es la mediatriz de la base, es decir, la otra diagonal.
En consecuencia, las diagonales son perpendiculares, y el paralelogramo formado por los puntos medios es un rectángulo.
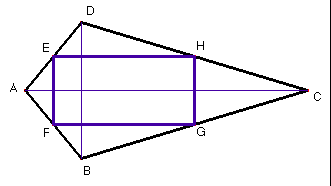
4. De tots els resultats anteriors se'n dedueix que les diagonals d'un estel són sempre perpendiculars.
5. Totes les propietats dels estels són també propietats del quadrat i del rombe donat que aquestes figures són casos particulars d'estels. Cerca propietats d'aquestes figures que no es compleixen als estels.
6. L'àrea d'un estel equival al semiproducte de les seves diagonals. Observa aquest resultat al dibuix de la figura que tens baix:
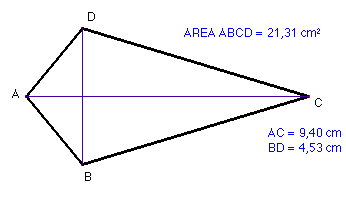
En els casos particulars del quadrat i el rombe, l'àrea és la meitat del quadrat de la diagonal donat que aquestes figures són casos particulars d'estels i tenen les diagonals iguals.
7. L'àrea d'un estel és la meitat de l'àrea del rectangle, per qualsevol posició del vèrtex G que es mou al llarg del costat del rectangle.
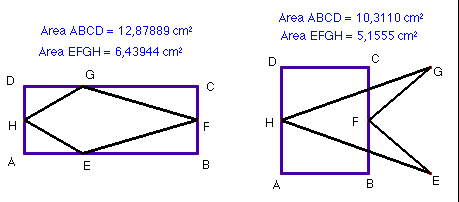
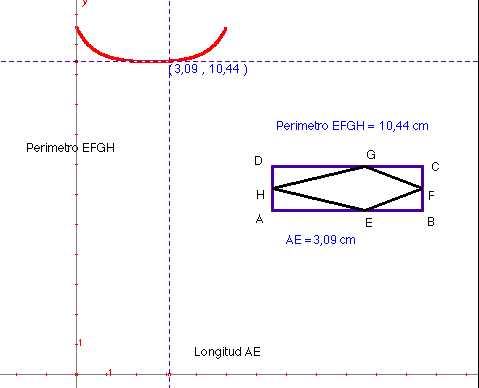
8. El perímetre va canviat mentre els punts E i G es mouen. Es farà mínim quan aquests vèrtexs es situïn als punts mitjos dels costats del rectangle, dit d'una altra manera, quan la figura sigui un rombe.
Una nube de puntos de los diferentes perímetros de EFGH en función de la longitud AE describirán una curva elíptica con el máximo cuando E coincida con A y D, es decir, cuando la cometa se convierte en un triángulo.
Si desitges l'arxiu i les imatges en format zip, CLIC AQUI