Introducció.
Geometria
Taller Matemàtiques – 2005
©Esteve Campins
Introducció.
Abans de començar diguem que la Geometria és segurament una de les branques més espectaculars i convenients en aquesta edat, donat que els objectes, els resultats i conceptes els podem "veure", cosa que no passa amb altres camps de la Matemàtica.
És una sort que avui dia disposem d’un munt d’eines per fer matemàtiques, feu una petita ullada a l’adreça:
http://users.libero.it/prof.lazzarini/voce03.htm
Les Altures d’un triangle.
En aquest primer exemple elemental practicareu les eines principals de construcció. La figura construïda constarà d’un triangle i les seves tres altures.
Trobareu també alguns exemples a Internet amb la interfície Cabri Java a l’adreça :
http://users.libero.it/prof.lazzarini/cabrijava01.htm
Entreu al programa amb l’executable Geomouse.exe que hi trobareu a la pàgina
http://www2.infotelecom.es/~ecampins/Matematiques/Aqui%20Matematiques.htmo també dins l'aula informàtica del centre a la carpeta :
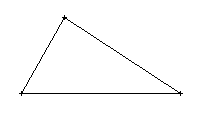
Amb la barra de botons de baix, empreu l’eina que dibuixa segments per dibuixar un triangle com el que teniu a continuació.
Ara, emprant el botó que dibuixa perpendiculars, dibuixeu les perpendiculars per cada vèrtex al costat oposat.
Dibuixa una perpendicular per un punt al segment que prèviament s’ha seleccionat.
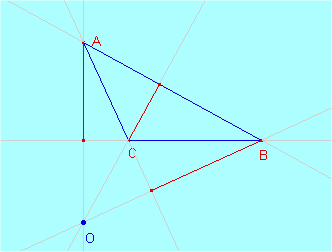
Obtindreu així una figura semblant a la que teniu aquí baix, l’alçada pel vèrtex B s’ha traçat amb un altre color per que es vegi millor:
Proveu vosaltres mateixos el mateix procediment amb un triangle molt més "pla" com el que teniu a l’exemple de baix:
Si teniu problemes amb els dibuixos, per exemple un costat us queda malament, una altura està mal dibuixada,...etc. podeu utilitzar la goma.
Esborra els diferents elements del dibuix quan ens hi col·loquem a sobre i cliquem amb el botó esquerra del ratolí.
Altres eines.
Per guardar els nostres dibuixos a la mateixa carpeta on està el programa i exemples preparats. Sembla que el programa contempla un màxim de dibuixos guardats. Proveu-ho vosaltres mateixos.
Dibuixa la perpendicular a un segment per un punt escollit per l’usuari.
Dibuixa segments. Escollim un primer punt, escollim un segon punt, i quan amollem el ratolí, Voilà ! Proveu vosaltres mateixos aquesta eina.
Dibuixa un angle qualsevol una volta triats el vèrtex i els altres 2-punts. La seva mesura en graus sexag. ens apareix al quadre de l’esquerra.
Dibuixa una perpendicular per un punt a un segment qualsevol. Primer ens demana els extrems del segment, desprès seleccionem el punt desitjat. Proveu aquesta eina abans de seguir fent pràctiques.
Dibuixa una paral·lela a un segment per un punt qualsevol del pla. Proveu també aquesta eina abans de seguir amb les pràctiques proposades més endavant.
El Teorema de Pitàgores.
Ens diu que els costats d’un triangle rectangle compleixen la relació:
a2 + b2 = c2
Construïu un triangle rectangle com el de la figura:
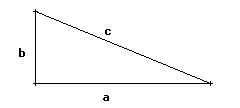
Mesureu amb la regla de baix les longituds dels costats i anoteu-les a un full de paper. Amb la calculadora, comproveu que compleixen la relació del Teorema.
Una simetria axial.
L’efecte és semblant a un mirall, cal però prèviament seleccionar l’eix de simetria per construir desprès la figura transformada.
Un cas senzill, la simetria d’un triangle qualsevol com el que teniu baix:
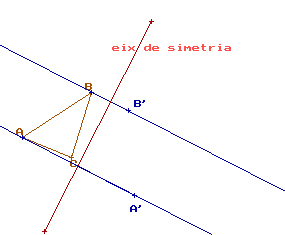
Cal primer que trobeu els vèrtex transformats A’, B’ i C’ fent les perpendiculars corresponents a l’eix de simetria. Empreu el fet que la distància de A a l’eix ha d’ésser la mateixa que la distància de A’ a l’eix de simetria. Semblant pels altres dos vèrtexs.
Si la figura a transformar és un
cercle, només cal cercar el transformat del centre. Fes un dibuix semblant al que teniu baix: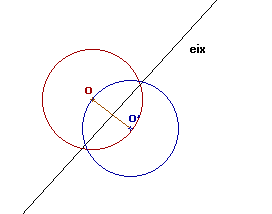
Explicació Geomètrica.
El teorema de Pitàgores ens diu bàsicament que un quadrat gran té àrea la suma de dos quadrats petits que tenen per costats els catets del triangle rectangle corresponent. Intenteu vosaltres mateixos un dibuix semblant al que teniu de mostra:
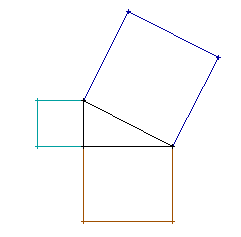
Objectes elementals.
En aquest apartat treballarem amb punts, segments, rectes i cercles.
Dibuixa un punt qualsevol a la pissarra de dibuix. Provareu també de dibuixar punts donant les seves coordenades.
Dibuixeu els punts de coordenades (-1,2) (3,4) i (5,-2) ( Pitgeu amb el ratolí al quadre de coordenades de dalt i entreu-les amb l’ordre corresponent. Observeu després el resultat )
Dibuixa un segment qualsevol del pla una volta donats 2-punts.
Uniu ara els punts anteriorment donats per observar el triangle resultant.
Nota: Desprès de pitjar el botó que dibuixa segments podeu utilitzar el quadre de diàleg de coordenades a la part de dalt esquerra per entrar els punts inicial i final del segment, obtindreu així més precisió.
Els dos botons dibuixen rectes. El primer, la perpendicular per un punt a un segment qualsevol. L’altra la recta paral·lela a un segment per un punt que desitgem.
Definiu vosaltres el centre de coordenades (0,0) i dibuixeu per aquest punt els eixos de coordenades cartesianes. ( Dues rectes perpendiculars que passin per aquest punt )
El compàs que dibuixa cercles. Cal triar un centre i un radi qualsevol i veureu aparèixer el cercle a la pissarra de dibuix.
Aquest botó ens permet treballar amb l’escala desitjada. Proveu vosaltres de fer algun canvi d’escala per veure l’efecte més gran o més petit de la figura.
Relacions.
Els objectes que constitueixen una figura solen estar lligats per relacions: la recta paral·lela a la recta t, el punt A intersecció dels costats a i b, El punt mig M d’un segment d’extrems A i B, ..etc.
Punt mig
d’un segment.
Dibuixeu un segment qualsevol d’extrems A i B i el seu punt mig M. Poseu els cartells corresponents amb el botó per posar text.
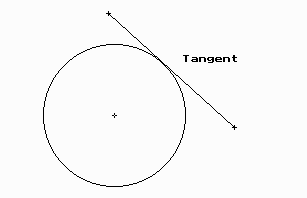
Recta tangent a un cercle.
Fixeu-vos que la recta dibuixada només tindrà un punt de contacte amb la circumferència dibuixada. Les altres posicions possibles són:
Secant. Dos punts de contacte amb el cercle.
Exterior. La recta i el cercle no tenen cap punt de contacte.
Ens esborra la pissarra sense guardar el dibuix a la carpeta de treball.
Calculadora.
El programa disposa també d’una calculadora amb algunes funcions bàsiques. Proveu-la per fer els càlculs proposats a continuació.
a) 3· ( 24 – 2’2) =
b)
Ö 5 + 2’4 =c) La tercera part del nombre
p = p : 3 =d) La meitat d’un angle de 45º = 45:2 =
__________________________________________________
El Quadrat inscrit.
Farem el cas del quadrat inscrit a un cercle, però hi ha altres casos com el quadrat inscrit a un altre quadrat.
Cal agafar per fer el dibuix dos diàmetres perpendiculars del cercle que escolliu a la pissarra de dibuix.
Indicacions:
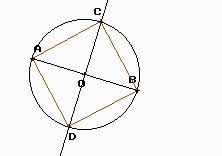
La Bisectriu d’un angle
.Per definició és la recta que divideix un angle en parts iguals. El programa no té cap eina específica per calcular la bisectriu, així doncs, haurem d’emprar el mesurador d’angles.
Us proposem que cerqueu i dibuixeu les bisectrius de 90º, 30º i 60º. A continuació teniu l’exemple de l’angle de 60º.
El mesurador d’angles. Cal pitjar aquest botó, seleccionar el vèrtex de l’angle i seguidament dos punts a sobre dels costats de l’angle de la figura.
Problema.
El programa ens pot servir per resoldre multitud de problemes geomètrics. Aquí en veurem un petit exemple.
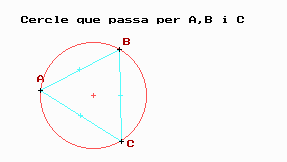
La circumferència que passa per 3 punts no alineats és única diu un conegut teorema. Ara bé, sou capaços de dibuixar-la ?
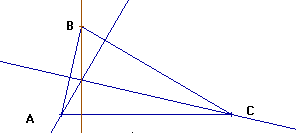
Proveu d’agafar tres punts qualsevols A, B i C ( no-alineats !) i dibuixeu les mediatrius dels segments AB, AC i BC. Obtindreu el centre de la circumferència donat que les tres rectes s’han de tallar a un punt.
Recordeu que aquesta eina serveix per trobar els punts mitjos dels segments AB, AC..
Et proposem també que facis el problema al revés:
Circumferència inscrita i circumscrita a un triangle.
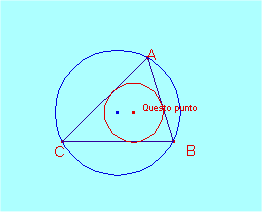
Indicacions:
" Le circonferenze sono concentriche quando, e solo quando, il triangolo è equilatero."
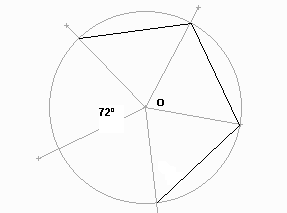
Angle central.
Una propietat prou senzilla dels cercles, l’angle pel centre sempre és doble que el traçat sobre un punt qualsevol del cercle.
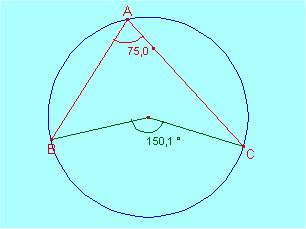
Moviments en el pla.
Les translacions, els girs i les simetries deixen les figures invariants. ( no varien la seva forma ni les seves dimensions )
En canvi les homotècies per exemple les fan més grans o més petites. Veurem uns exemples de cada tipus de moviment.
Simetries.
Una simetria inverteix l’ordre dels vèrtex d’un polígon, en canvi, no en modifica la forma ni les dimensions.
Bàsicament n’hi ha de dos tipus :
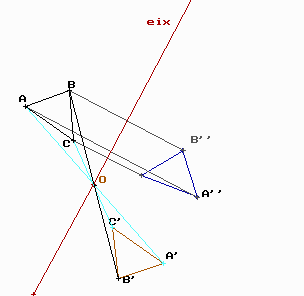
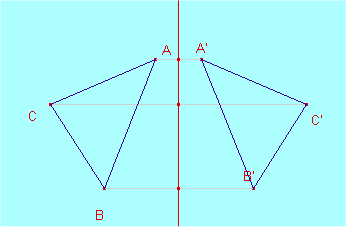
A la simetria axial, els punts A, A" disten el mateix de l’eix de simetria. El mateix amb els altres vèrtexs.
Nota: La distància d’una recta a un punt exterior s’agafa damunt la perpendicular pel punt a la recta.
Veure el dibuix:
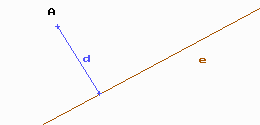
Exercicis
1. Calcula la distància del punt A=(-1,3 ) a la recta que passa pels punts B=(2,5) i C=(3,-2)
2. Dibuixa les rectes que passen per AB i BC. Calcula aprox. La distància de l’0rigen de coordenades (0,0) al punt d’intersecció de les rectes.
3. Dibuixa la figura transformada del segment AB de la figura fent una simetria axial que té per eix la bisectriu del 1r quadrant del sistema de coordenades.
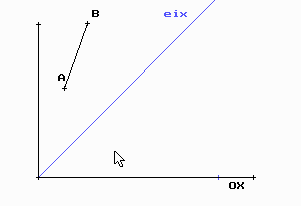
4. Dibuixa la figura transformada del polígon de baix fent una simetria central de centre l’origen de coordenades (0,0)
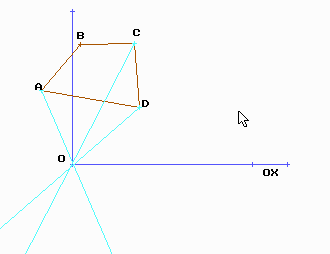
5.Fes una simetria axial d’un quadrat qualsevol agafant com l’eix OX l’eix de simetria.
Vectors en el pla.
Un vector és senzillament un segment orientat, quan diem el vector AB ens referim al tros de recta que parteix de A i arriba a B.
Els vectors ens permeten per exemple com es farà la translació de les figures ( en quin sentit i direcció i amb quina distància ).
Proveu de dibuixar el vector d’extrems AB on A=(-1,2) i B=(2,1)
Us quedarà exactament igual que un segment com els que havíem dibuixat fins ara.
Translacions.
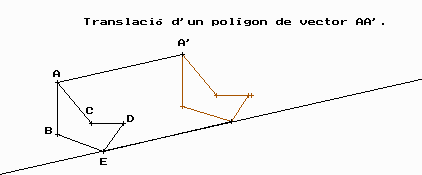En aquests moviments cal indicar un vector ( que ens dona la direcció i el sentit, així com la distància que la figura serà traslladada )
Teniu un exemple a l’esquerra del text.
Recordeu aquesta eina, serà necessària per traçar les paral·leles al vector de translació pels punts B, C, D.
Exercicis
1.Fes una translació d’un cercle qualsevol de vector AB=(-1,3)
2.Fes una translació de longitud 12 cm. paral·lela a l’eix OX d’un pentàgon.
Girs.
En els girs, cal un centre de gir (un punt) i naturalment un angle de gir ( que sempre que sigui + entenem en el sentit de les agulles d’un rellotge ).
És un tipus de moviment directe. Dit d’una altra manera, no canvia l’orientació dels vèrtexs dels polígons.
Exemple:
Gir d’un triangle de centre l’origen (0,0) i angle 60º
Observeu que els vèrtex A i A’ es troben a un cercle de centre l’0rigen de coordenades (el centre de gir). El mateix passa amb els altres vèrtexs dels dos triangles, original i transformat pel gir.
Cal aquí emprar el compàs per traçar els cercles auxiliars i també el traçador d’angles per marcar els angles corresponents de 60º
Dibuixa l’angle corresponent una volta fixem el vèrtex i desprès els altres dos punts. El valor de l’angle va variant a mesura que col·loquem el tercer punt. (el veiem a la part esquerra de dalt la pissarra de dibuix)
Activitats.
1. Fes una translació del paral·lelogram de vèrtexs A=(1,1) B=(4,2) C=(5,4) i D=(2,3) agafant com a vector de translació
2. Dibuixa un quadrat ABCD de 3cm. de costat.
Prolonga la diagonal AC fins a un punt M, de manera que AM =2AC
Fes ara un gir del quadrat de 60º agafant com a centre el punt M.
3.
Dibuixa la figura transformada del polígon que tens baix per una simetria central decentre el punt M=(2,1)
Recorda que els vèrtexs transformats estan sobre la recta que els uneix amb el centre M de simetria i a més d(C,M)=d(C’,M).
La mateixa condició pels altres vèrtexs.
d(A,M)=d(A’,M)
d(B,M)=d(B’,M)..etc.
4. Dibuixa els punts de coordenades A=(2,5) B=(4,2) i C=(10,6)
Uneix ara els punts i demostra (emprant el mesurador d’angles) que són els
vèrtexs d’un rectangle.
Troba tu mateix l’altre vèrtex i acaba el dibuix del rectangle.
5. Els punts A=(-10,7) B=(-3,8) C=(2,3) i D=(-5,2) són els vèrtexs d’un rombe ( Té les diagonals perpendiculars )
Fes una simetria axial d’eix OX i trobaràs la figura transformada. (naturalment ha d’ésser també un rombe)
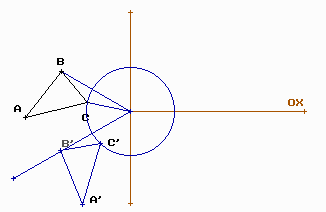
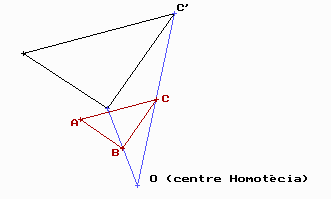
Homotècies.
Són moviments que amplien o redueixen les figures planes conservant la seva forma.
Ens donen un centre d’homotècia O ( que estarà alineat amb qualsevol vèrtex i el seu transformat ) i una raó (un nombre o en forma de percentatge) que ens indicarà per quina quantitat cal multiplicar les distàncies dels vèrtexs al centre O.
Exemple:
Una homotècia d’un triangle de raó = 2
El centre, un vèrtex i el seu transformat estan alineats. Les distàncies dels punts al centre d’homotècia són sempre proporcionals de raó = 2.
OC’ = 2·OC
OB’ = 2·OB
OA’ = 2·OA
Activitats.
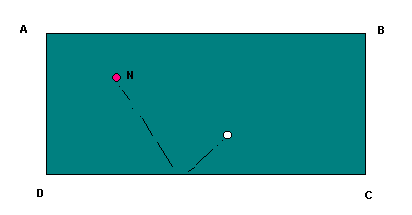
6. Si M i N són dues boles de billar. Calcula aproximadament i per tempteig ( els angles d’incidència i rebot a la banda han d’ésser iguals ) la trajectòria de la bola blanca M tocant la banda DC per xocar després amb la bola N.
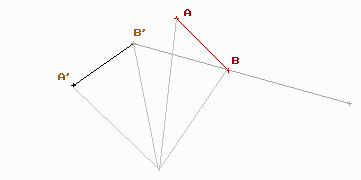
7. Calcula l’angle i el centre de gir que transforma el segment AB en el segment A’B’ de la figura que tens baix:
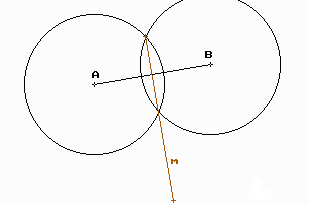
8. Dibuixa dos cercles de radis diferents que es tallin a 2 punts. Dibuixa també la recta que uneix els seus centres O1 i O2. Dibuixa també el punt mig del segment O1O2.
9. Dibuixa un quadrat qualsevol ABCD. Agafa el centre (0,0) com a punt de referència d’una homotècia de raó = ½. Dibuixa la figura transformada.
10.Dibuixa un pentàgon regular ( 5 costats tots de la mateixa mesura ).
Indicació: parteix d’un cercle qualsevol i el divideixes amb 5 angles iguals partint del centre del cercle.
Fes el mateix amb un hexàgon i un polígon regular de 10 costats.
Eines de mesura.
El mesurador d’angles i la regla ens permeten trobar les mesures de qualsevol polígon.
Mesura la longitud d’un segment.
Mesura un angle qualsevol quan indiquem amb el ratolí el vèrtex seguit dels seus extrems. L’angle ens apareix en graus a la part de dalt esquerra de la pissarra de dibuix.
Mediatriu.
Una altra manera de trobar la recta perpendicular que passa pel punt mig d’un segment qualsevol d’extrems A i B
Paralel·logram
És un polígon de 4 costats paral·lels dos a dos. Donats 3 punts qualsevols A,B i C sempre hi passa per ells un paral·lelogram.
Proveu vosaltres de partir de 3 punts qualsevols i trobar el 4t vèrtex per completar la figura.
És força interessant que proveu l’animació Java de la pàgina del Cabri, que ens permet observar clarament la propietat de l’exercici que segueix.
http://users.libero.it/prof.lazzarini/cabrijava04.htm
El paral·lelogram inscrit.
Ara resulta que si ajuntem els punts mitjos dels costats de qualsevol quadrilàter resulta ser un paral·lelogram. !
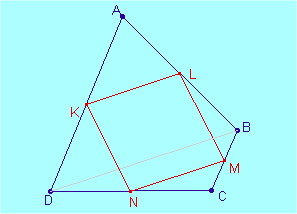
" i triangoli ALK e ABD sono simili avendo un angolo in comune compreso tra lati proporzionali, analogamente sono simili i triangoli CNM e CDB; ne segue che i lati KL e MN sono entrambi paralleli al lato BD e dunque paralleli tra loro "
Indicacions:
Pitàgores.
El teorema es comprova fàcilment si dibuixeu un triangle rectangle isòsceles. Per exemple podeu agafar 2 segments perpendiculars de longitud 3 cm.
Si ara mesureu la hipotenusa comprovareu que us dona aprox.
Ö 18 @ 4’2426...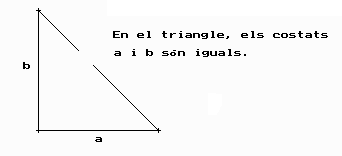
L’arrel quadrada.
Hi ha una construcció geomètrica senzilla que permet representar l’arrel d’un nombre qualsevol a.
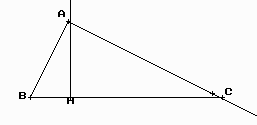
Mesureu vosaltres el segment HC i l’altura del triangle. Aquesta haurà d’ésser aprox. L’arrel quadrada del segment HC.
Naturalment quan el segment HC té una arrel exacta, el procés és molt més clar.
Teorema di Viviani.
És interessant que proveu de dibuixar algun cas concret amb el programa Geomouse i comproveu que es compleix que donat un punt qualsevol P, la suma de distàncies als costats d’un triangle equilàter és sempre constant.
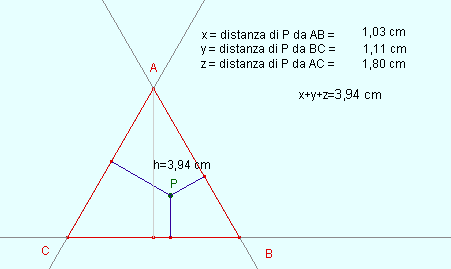
També és interessant que visiteu la pàgina
http://users.libero.it/prof.lazzarini/cabrijava18.htm i seguiu les animacions Java juntament amb els càlculs movent pel pla el punt P dins el triangle.
