Introducció.

Des de que els grecs van inventar les Matemàtiques com a disciplina, la essència dels nombres ha estat un aspecte molt atractiu pels estudiosos de totes les èpoques. Des de la seva classificació, recerca de nombres amb característiques especials ( primers, cap-i-cua, amics, perfectes, etc.), fins l'estudi de les seves propietats, aquests problemes han fascinat als matemàtics; fins i tot alguns han escrit el seu nom a l'historia per la seva relació amb els nombres, traspassant els límits del mon matemàtic, com els casos evidents de l'escola pitagòrica, Pierre de Fermat o Srinivasa Ramanujan.

Molts pensem que l'èxit d'aquest tipus de problemes radica en que són entreteniments que es basen en operacions aritmètiques conegudes per la majoria de la població, encara que la seva solució no és evident, a més alguns porten bastant complexitat afegida en la seva resolució.

Hi ha alguns centres de Secundària que ja tenen materials publicats prou dignes, de tota manera trobem també materials al weib.caib.es, pntic.mec.es, www.xtec.es, i altres servidors com els de les diferents facultats de matemàtiques a tot l’estat.

Per a nosaltres com a professors, aquests problemes tenen característiques didàctites interessants com les següents:

• Són força motivadors.

• Serveixen per introduir qualsevol tema del “bloc numèric”.

• Complementen i reforcen el tema de nombres de la ESO.

• Agilitzen el càlcul mental amb nombres.

L’objectiu d’aquesta unitat didàctica és donar una petita mostra del que s’hi pot trobar, i de passada, comentar i practicar amb aspectes d'alguns d'ells d'una manera autònoma i interactiva.

Vegem a continuació una petita selecció proposada per aquells alumnes del Centre matriculats a la matèria de Taller de Matemàtiques de 2n ESO.

Set nombres a la Y grega.

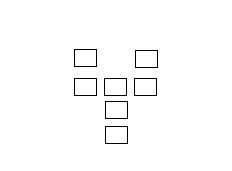
Col·loca les xifres del 1 al 7 en el tauler que tens a continuació, de manera que dos nombres consecutius no estiguin junts ni en horitzontal, vertical o en diagonal.

La roda numèrica.

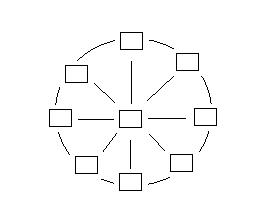
Col·loca els nombres del 1 al 9 en els quadres, de manera que totes les files de tres nombres sumin 15.

El triangle equilàter.

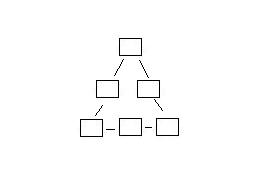
Distribueix les xifres del 1 al 6 de manera que la suma de cada costat doni el mateix.

El quadre de nombres.

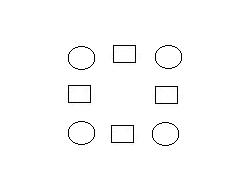
Col·loca els vuit primers nombres al tauler, de manera que cadascun que estigui a un quadrat sigui la diferència del que estan als cercles veïns.

Fila numèrica.

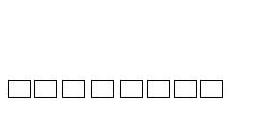
Col·loca les xifres del 1 al 8 en els quadres de manera que la diferència en qualsevol ordre entre dos veïns no sigui mai més petita que 4.

Parells i senars.

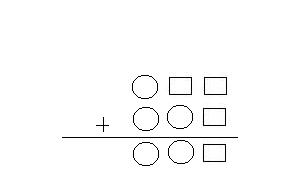
Amb els nombres del 1 al 9 fes la suma que apareix en el tauler, col·locant els nombres parells en els quadrats i els senars en els cercles.

La serp.

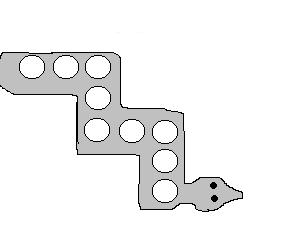
Situa sobre els cercles els nombres del 1 al 9, de forma que cada línia de tres nombres suma 13.

El producte de 9 nombres.

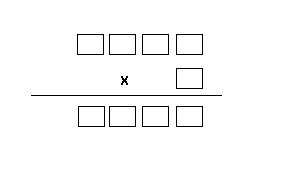
Col·loca les xifres del 1 al 9 de manera que el resultat sigui correcte.

Nota.

La majoria de jocs admeten diverses solucions. En el segon es pot variar les condicions dient que la suma sigui la mateixa. En el tercer hi ha solucions per suma 9, 10, 11 i 12. El quart s'ha presentat com a diferència però es pot fer el mateix de manera que en els quadres hi hagi la suma dels veïns.

© Revista Suma – Febrer 2002