Introducció.

La quantitat de materials publicats a la xarxa Internet augmenta diàriament, basta teclejar la frase “Matemàtiques” a un qualsevol dels motors de recerca disponibles i ens apareix gran quantitat d’enllaços a pàgines amb continguts educatius, d’empresa, ...etc.

Hi ha alguns centres de Secundària que ja tenen materials publicats prou dignes, de tota manera trobem també materials al weib.caib.es, pntic.mec.es, www.xtec.es, i altres servidors com els de les diferents facultats de matemàtiques a tot l’estat.

L’objectiu d’aquesta unitat didàctica és donar una petita mostra del que s’hi pot trobar, i de passada, comentar i practicar amb aspectes de la matèria d’una manera autònoma i interactiva.

Software.

Per sort, avui dia hi ha altres maneres de “fer matemàtiques”, per exemple l’ús d’eines tant potents com les calculadores científiques, amb capacitats gràfiques i els diferents programes d’ordinador que permeten fer un munt de coses.

Algunes adreces per trobar programes les tens baix:

Software de Matemàtiques

Història de les Matemàtiques.

Segur que existeixen quantitat d’articles publicats a Internet. Nosaltres hem provat una pàgina que ens agradat bastant, http://platea.pntic.mec.es/~aperez4/html/presentacion.html

Babilonia

Desde el tercer milenio antes de Cristo los pueblos que habitaron entre los ríos Tigris y Eúfrates nos han dejado miles de tablillas de arcilla. En más de 500 de ellas apaprecen manifestaciones matemáticas que nos han permitido descubrir desde su sitema de numeración en base 60 a sus conocimientos sobre el teorema de Pitágoras.

De su afición a las observaciones astronómicas acerca de las posiciones de los planetas observables a simple vista Mercurio, Venus, Marte, Júpiter y Saturno conservamos en la actualidad dos vestigios muy populares: el horóscopo y el sistema sexagesimal.

- El horóscopo. Eran excelentes astrólogos, ellos bautizaron las doce constelaciones del zodíaco, dividiendo cada una de ellas en 30 partes iguales.
Es decir, dividieron el círculo zodiacal en 12 x 30 = 360 partes.

- El sistema sexagesimal. De ellos hemos heredado la división de la circunferencia en 360 grados y la de cada grado en 60 minutos y cada minuto en 60 segundos. Y la patente de nuestra manera de contar el tiempo también es suya.

- Algoritmos. Contaban con un algoritmo para calcular raíces cuadradas, trabajaban con fracciones, resolvían ecuaciones de primer y segundo grado e incluso algunas ecuaciones cúbicas de la forma

n³ + n² = a a: entero positivo cualquiera.

- Sistemas de numeración. A partir del año 2.000 a de C, descubren las ventajas de un sistema posicional, que les permite escribir cualquier número con sólo dos símbolos T para el 1 y < para el 10.
La base que utilizan es 60.

24 = <<TTTT

93 = 60 + 30 + 3 = T<<<TTT

Hoy en día los que más utilizamos en la era moderna es el sistema decimal o de base 10 i el sistema binario ( para transmitir i manejar información digital, que maneja sólo dos símbolos el cero i el 1 ).

Así en sistema binario :

decenas: 2¹ = 2

centenas: 2² = 4

millares: 2³ = 8

diez mil: 2⁴ = 16

.

.

i en general

10ⁿ : 2ⁿ = potencia de dos correspondiente.

Ejercicio:

Averigua los números que corresponden a las tiras binarias que aparecen abajo indicadas:

101 = 4 + 0 + 1 = 5

10101 = 16 + 0 + 4 + 0 + 1 = 21

11010111 =

10110010 =

- El teorema de Pitàgoras. La tablilla conocida como Plimpton 322 que se conserva en la Universidad de Columbia, escrita hacia el año 1800 antes de Cristo en la que aparecen cuatro columnas de números distribuidos en 15 filas. En apariencia podía tratarse de algún tipo de anotación contable pero descifrados los números corresponden a la primera relación de ternas pitagóricas de la que se tenga conocimiento.

Egipto

Según Herodoto los egipcios son los padres de la Geometría, pero gracias a sus monumentos y sus papiros también sabemos hoy que disponían de un sistema de numeración adicional que les permitía trabajar con fracciones de una forma muy especial ya que el numerador siempre era la unidad.

El papiro egipcio es menos resistente al paso del tiempo que las tablillas babilonias.

Sin embargo alguno ha llegado hasta nosotros. Los más populares el papiro de Rhind y el de Moscú. En ellos aparece una colección de más de 100 problemas que nos brindan una valiosa información de las matemáticas egipcias.

Su sistema de numeración era de base diez, como el nuestro. Los símbolos para representar las potencias de 10 eran los que aparecen en la imagen.

- Papiro de Rhind.

Los egipcios, como los babilonios, también trabajaban con fracciones, con partes de la unidad.

Pero lo curioso es que sólo utilizaban fracciones con numerador la unidad, es decir de la forma: 1/2, 1/3, 1/4, 1/7, 1/15, 1/47...

Cualquier parte de la unidad la expresaban como suma de fracciones de este tipo.

El papiro de Rhind contiene una tabla de conversión de partes de la unidad a estas fracciones. Es el equivalente con más de 3.000 años de antigüedad de nuestras tablas de multiplicar, sólo que para trabajar con fracciones.

Grecia y Roma.

Pitágoras.

La figura de Pitágoras está envuelta en un halo de leyenda, misticismo y hasta de culto religioso. Y no es tan extraño si pensamos que fue contemporáneo de Buda, de Confucio y de Lao-Tse (los fundadores de las principales religiones orientales)

El término "matemática", al igual que el de filosofía, se le debemos a él.

¿Cuáles son las principales aportaciones matemáticas de la escuela pitagórica?...
La primera y quizás la más importante el introducir la necesidad de demostrar las proposiciones matemáticas de manera inmaterial e intelectual, al margen de su sentido práctico. Los pitagóricos dividieron el saber científico en cuatro ramas: la aritmética o ciencia de los números - su lema era "todo es número" -, la geometría, la música y la astronomía.

Pitágoras descubrió que existía una estrecha relación entre la armonía musical y la armonía de los números.

Si pulsamos una cuerda tirante obtenemos una nota. Cuando la longitud de la cuerda se reduce a la mitad, es decir en relación 1:2 obtenemos una octava.

Si la longitud era 3:4 obtenemos la cuarta i si la longitud es 2:3 tenemos la quinta.

Pero lo que colmó de gozo a Pitágoras, hasta el punto de mandar sacrificar un buey a los dioses, fue la demostración del famoso teorema:

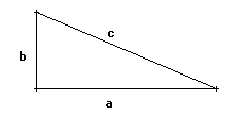
c² = a² + b² En todo triàngulo rectángulo. Donde c es la hipotenusa i a, b los otros lados del triángulo.

Por desgracia, el secreto que imponía las normas de la sociedad ha hecho imposible que esta demostración llegue a nuestro conocimiento, aunque podemos deducir que no sería muy distinta de la que Euclides nos brinda en sus “Elementos de Geometria Plana”.

Sin duda es el teorema que cuenta con más número de demostraciones.
Scott Loomis reunió y publicó a principios de este siglo 367 demostraciones.

Números poligonales.

Hipsicles de Alejandría ( S.II a. de C.) va a proporcionar la definición de número poligonal de d lados y orden n de una forma que algebraicamente equivale a nuestra fórmula :

N (n,d) = n + 1/2 n ( n -1) ( d -2 )

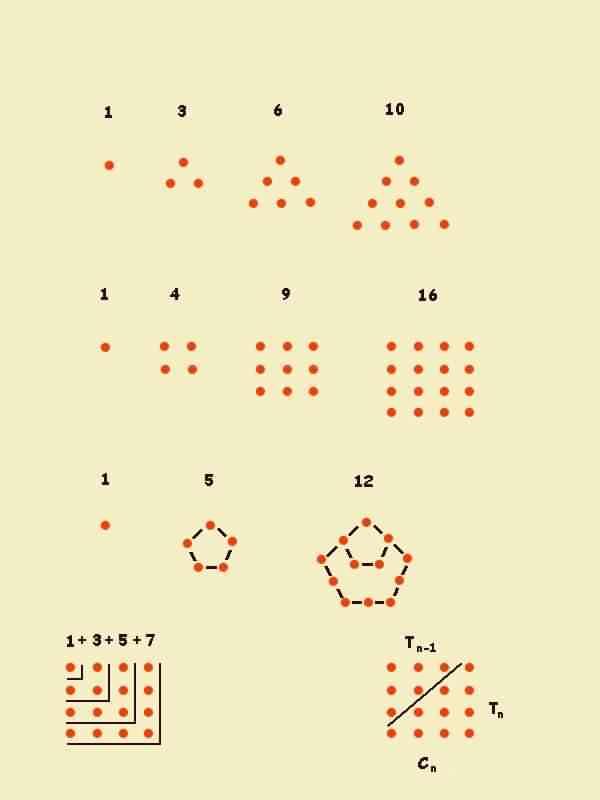
Euclides en el libro más famoso de la Historia de las Matemáticas recoge gran parte de los conocimientos Pitagóricos sobre los números y define los números primos y compuestos de forma geométrica: un número entero es compuesto cuando tiene divisores distintos de él mismo y de la unidad, es decir cuando se puede dibujar como un rectángulo numérico.

Por ejemplo, los números 6 i 14 són compuestos. Se puede dibujar una cuadrícula de 2x3 filas i columnas i se puede dibujar una cuadrícula de 2x7 filas i columnas respectivamente:

El 6 = 2 filas x 3 columnas.

Números perfectos

En el libro IX de los Elementos Euclides nos deja perplejos con su proposición 36, que proporciona un método original para encontrar números perfectos.

Def. Un número es perfecto cuando es suma de sus divisores propios. Por ejemplo el 6 es perfecto 6 = 1 + 2 + 3.

"Si la suma de las n primeras potencias de 2 es un número primo, entonces el producto de la suma por la última potencia sumada es un número perfecto".

Si (1+2+2²+...+2ⁿ) es primo,
entonces (1+2+2²+...+2ⁿ)·2ⁿ es perfecto

Nicómaco de Gerasa.

En su “Introductio Arithmeticae” incluye los 4 primeros números perfectos: 6, 28, 496, 8128

Nicómaco llegó a descubrir resultados generales de interés como el hecho de que:

“El cubo de todo número entero n, es la suma de n números impares consecutivos: “

1³ = 1;

2³ = 3+5;

3³ = 7+9+11; ...

Es decir, ya en el siglo I encontramos la solución a uno de nuestros problemas:

1³ + 2³ + 3³ + ... + n³ = 1 + 3 + 5 + 7 + 9 + 11 +...= (1+2+3+...+n)²

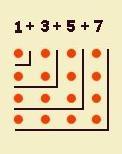
Comprova tu mateix la igualtat anterior per un nombre relativament petit, per exemple per n= 5

Resulta curiós que desde temps tan antigs es coneguin resultats numèrics relativament profunds com aquest i que encara avui en dia ens sorprenen.

Demana al teu professor si coneix alguna fórmula per sumar nombres que estan en progressió aritmètica, com per exemple:

1 + 3 + 5 + 7 + ... + (2n+1) = ?

En la época Griega tenemos ya por lo tanto matemáticos notables, algunos famosos como Apolonio (padre de las cónicas), Arquímedes, Ptolomeo o Diofanto que enuncia diferentes problemas numéricos cuya solución ha llegado hasta nuestros días.

Diofanto

La Aritmética constaba de 13 libros de los cuales sólo seis sobrevivieron a la destrucción de la gran biblioteca de Alejandría, primero por los cristianos y luego por los musulmanes. En él Diofanto propone más de cien problemas numéricos y da brillantes soluciones a todos ellos.

En 1621 aparece en Francia una traducción al latín de estos seis libros, realizada por Bachet.

Números romanos.

El sistema de numeración romano, esas cifras que aún hoy vemos en muchos de nuestros monumentos, no es una buena herramienta para el cálculo.

Utiliza letras del alfabeto para representar los números y no es posicional, es decir cada símbolo vale siempre lo mismo, no importa dónde esté colocado.

Las cifras que utilizaban son éstas: I, V, X, L, C, D, M

El sistema es basa en la suma dels símbols. Llevat del cas que un símbol de valor menor vagi col·locat abans que un símbol de valor major.

Per exemple:

1336 s’escriu MCCCXXXVI

Però 2894 és: MMDCCCXCIV

Donem ara un gran salt en la història i passem a parlar una mica del segle passat, cuna de matemàtics notables que ens han deixat entre altres coses la notació moderna i universal que empren els matemàtics actuals.

Naturalmente la tabla anterior es sólo una muestra, muchos más han llegado a nuestros días procedentes del siglo XIX. Se han introducido también otros surgidos de nuevos conceptos matemáticos de nuestros días.

El siglo XIX

Gauss.

Junto a Arquímedes y Newton, Gauss es sin duda uno de los tres genios de la historia de las Matemáticas. Sus aportaciones en todos los campos matemáticos fueron increíbles, aunque algunos de sus descubrimientos tuvieran que esperar más de un siglo para ser valorados debidamente.

Las aportaciones de Gauss en todos los campos de la Matemática son inestimables: Teoría de números, Astronomía, Magnetismo, Geometría, Análisis... Cualquier gran descubrimiento matemático a lo largo de este siglo encuentra detrás la alargada sombra de Gauss.

Sólo en Francia otra figura es capaz de hacerle sombra, Cauchy, dando paso, o mejor obstaculizando, a dos jóvenes genios: Abel y Galois.

Cauchy (1789-1857)

Cauchy dió al cálculo diferencial la forma que tiene hoy.
Precisando con rigor la noción de límite y de continuidad tal como las utilizamos en la actualidad.

Lecciones de cálculo infinitesimal (1823), Ecuaciones diferenciales, Funciones de variable compleja, Álgebra, Física Teórica...

Sin embargo la Historia de las Matemáticas no le perdonará su poca atención a las memorias presentadas por Abel y Galois a la Academia de Ciencias...

Galois (1811-1832)

Un dels matemàtics més joves que arriba a resultats importants en el camp de la matemàtica com per exemple el famós teorema fonamental de l’Algebra.

"Una ecuación irreducible de grado primo es resoluble por radicales si y solo si todas sus raíces son funciones racionales de dos cualesquiera de las raíces"

Va morir també molt jove producte d’una malaltia que avui dia es cura amb antibiòtics sense més problema.

Abel (1802-1829)

Interessat també entre altres coses per la resolució algebraica d’equacions amb una variable, fa també les seves aportacions. Algunes notes i treballs publicats han arribat fins els nostres dies, guardats gelosament pel govern francès.

Memoria "Sobre la Resolución Algebraica de Ecuaciones". 1824

"No existe una fórmula general expresada en términos de operaciones algebraicas explícitas entre los coeficientes que nos dé las raíces de la ecuación si el grado es mayor que 4"

Dos jóvenes matemáticos, uno húngaro János Bolyai, y otro ruso Nokolai Lobachevsky, publicaron casi simultáneamente su descubrimiento de esta geometría hiperbólica.

Veinte años antes, Gauss había llegado a esos mismos resultados, aunque nunca se atrevió a publicarlos.

Del mismo siglo son también Sofía Khovalevskya (1850-1891) una de las pocas jóvenes matemàticas de la época, Riemann (1826-1866) Fundamentos para una teoría general de las funciones de una variable compleja. (1851)

"Las Hipótesis que sirven de fundamento a la Geometría": Las geometrías no euclídeas no elementales, Conjetura de Riemann: "Todos los ceros complejos de la función zeta tienen parte real igual a 1/2"

ÓNota.

Els textos en castellà d’aquest document pertanyen íntegres al material publicat per

ANTONIO PÉREZ SANZ a la seva pàgina web :

http://platea.pntic.mec.es/~aperez4/

Ens falta encara una altra gran figura d’aquest segle XIX, David Hilbert (1862-1943)

Les seves contribucions son també rellevants, sobretot també en l’aspecte dels problemes que va formular en el seu moment ( indicant també de vegades la possible solució ) i que han portat a altres matemàtics de cap al llarg del temps.

Los famosos 23 problemas de Hilbert, uno de los culpables de que hoy estemos aquí celebrando, 100 años más tarde del famoso Congreso de París, el 2.000 AÑO MUNDIAL DE LAS MATEMÁTICAS.

Part d’aquest material pretén ésser també una petita contribució a difondre part de la història d’aquesta ciència patrimoni de tota la humanitat i que ens ha permès fites notables que fa dos segles mai ens haguérem imaginat.

“Para muchos, las matemáticas constituyen un Universo abstracto, extraño y lejano, patrimonio de unos pocos genios. Un mundo alejado de la realidad de cada época con una existencia independiente al devenir de la historia. Nada más lejos de la realidad.

A lo largo de esta conferencia veremos que en cualquier momento histórico las ideas matemáticas que se han desarrollado han pretendido responder a los problemas concretos de cada época.

Problemas que en la mayoría de los casos provienen de actividades tan dispares como el comercio, la agricultura, la astronomía, la navegación, la guerra... y en épocas más recientes la Física, la Medicina, la Biología, la Economía, la Sociología, la Ingeniería... “

“Podremos participar en un viaje organizado, con excursiones en el tiempo y en el espacio para perseguir las grandes ideas matemáticas y visitar a los personajes que las han producido:

Pitágoras, Euclides, Ptolomeo, Arquímedes, Apolonio, los Bernouilli, Newton, Descartes, Leibniz, Cardano, Euler, Gauss, Laplace...”

Pitágoras.

Nació: en el siglo VI A.C. (probablemente 569). en la isla de Samos.(hoy Grecia)
Murió: en el siglo V A.C. en Crotona (hoy Italia).

Euclides.

(fl. 300 a.C.), matemático griego, cuya obra principal, Elementos de geometría, es un extenso tratado de matemáticas.

Arquímedes.

(287-212 a.C.), notable matemático e inventor griego, que escribió importantes obras sobre geometría plana y del espacio, aritmética y mecánica.

Apolonio de Perga.

Matemático griego, llamado el 'Gran Geómetra', que vivió durante los últimos años del siglo III y principios del siglo II a.C.

Más información en http://euler.us.es/~libros/griegos.html

DE LA ARITMÉTICA MEDIEVAL AL

ÁLGEBRA RENACENTISTA.

Tras la caída del Imperio Romano de Occidente siguió un periodo, del siglo VI al XIV, oscuro para la matemática; únicamente brillaron los matemáticos del Islam y, en menor medida, algunas otras figuras, Boecio, Fibonacci, Bradwardine, Nemorario, aunque de calidad muy inferior a los griegos. Boecio era un romano de familia noble. Estudió en Atenas filosofía y matemáticas. A su regreso a Roma fue nombrado senador y sin causa aparente fue encarcelado y ejecutado en el 524 d.C. En la soledad de la cárcel escribió su obra “De consolatione philosophiae” que lo haría inmortal. Antes, sin embargo, había escrito distintas obras menores sobre aritmética, geometría, música y astronomía. Eran obras elementales fáciles de entender que fueron bastante populares en la Edad Media. 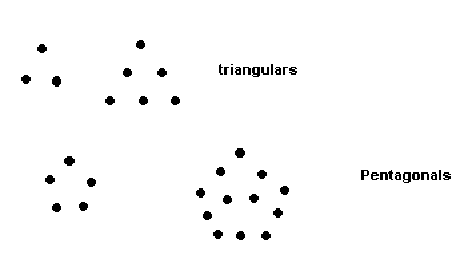Incluimos aquí un incunable de la Opera de Boecio del año 1492 donde podemos apreciar los números poligonales como n(n+1)/2 - números triangulares- y los 3n(n-1)/2 - números pentagonales -

Lo más importante de este periodo fue la difusión y consolidación de nuestro actual sistema de numeración hindú - árabe, especialmente útil para las actividades comerciales. Por esto, fue en las activas repúblicas alemanas e italianas donde, ya en el Renacimiento, se produjo la mayor profusión de aritméticas: la de Francesco Pellos, Luca Pacioli, Stiefel Este último fue un personaje singular. Se ordenó monje en Esslingen, su ciudad natal en 1511, luego durante los años de la Reforma se convirtió en seguidor de Lutero y estudiando la Biblia comenzó a interesarse por una combinatoria numérica. Una de las anécdotas más curiosas ocurrió cuando, basado en su misticismo numérico, comenzó a predicar el fin del mundo para el 18 de octubre de 1511 estando a punto de ser linchado por sus seguidores al no ocurrir nada ese día.

En 1544 después de 9 años de estudio sistemático de la Matemática publica su “Arithmetica integra” donde mejora la representación de las potencias de la incógnita en una ecuación y utiliza por primera coeficientes negativos sin embargo, incomprensiblemente, seguirá ignorando las soluciones negativas de una ecuación.

ÓNota.

Els textos en castellà d’aquesta part pertanyen íntegres al material publicat per

Renato Alvarez Nodarse (ran@us.es).

http://euler.us.es/~libros/index.html

Pero sin duda alguna, el mayor logro matemático del siglo XVI fue la resolución por radicales de las ecuaciones de tercer y cuarto grado. En cuatro mil años, desde que los babilonios descubrieran como resolver la de segundo grado, casi nada nuevo se había logrado en este campo. La historia de la resolución de las ecuaciones de tercer y cuarto grado tiene, además, todo el colorido de la época: intrigas, desafíos públicos, acusaciones de plagio. Sus protagonistas, Tartaglia y, sobre todo, Cardano, médico, matemático, filósofo, escritor y astrólogo, representan fielmente las miserias y virtudes del hombre renacentista.

Activitats.

• Escriu en nombres romans els 59 i el 73. Recorda que amb la seva notació els símbols de menor valor es resten del que va immediatament desprès.

Així :

83 = LXXXIII

102 = CII

1942 = MIMILII

• Escriu i dibuixa els cinc primers nombres triangulars i pentagonals. Recorda com anaven fent una ullada al gràfic de baix:

• Recordes la definició de nombre primer ? ( No té divisors llevat de la unitat i ell mateix )

Apuntat al club “Eratóstenes” anant a la pàgina:

http://www.xtec.es/~jjareno/totmm/club/club_deratostenes.htm

Hauràs d’omplir també el teu formulari com a soci del club que trobaràs dins la mateixa carpeta de treball club.doc

Per comprovar els teus nombres primers, ves a la pàgina Primers.htm

• Fes tota la unitat didàctica sobre el Teorema de Pitàgores que hi trobaràs a la mateixa carpeta de treball:

Descartes\1y2_eso\Teorema_de_Pitagoras\index.htm

• Fes la unitat didàctica sobre els Triangles que trobaràs també a la carpeta de treball:

Descartes\1y2_eso\Triangulos\index_tri.htm

ÓNota.

Els materials del programa Descartes pertanyen als autors que figuren a la URL de baix. Si vols, els trobaràs integres a la adreça:

http://www.cnice.mecd.es/Descartes/descartes.htm