1. Els Nombres.

Al llarg de la història l’home ha utilitzat nombres per contar, per mesurar i fer previsions. Durant el curs veuràs diferents tipus de nombres i també tota una sèrie d’operacions possibles amb ells. Començant per les mesures senceres, passant per les racionals que ja utilitzaren els grecs per mesurar longituds i acabant amb tot tipus de nombres reals on la seva part decimal moltes vegades no és totalment coneguda.

Els Naturals.

• Els nombres naturals 1, 2, 3, 4,….15 serveixen per comptar i per ordenar. Naturalment n’hi ha infinits i per diferenciar-los d’altres nombres els agrupem a un conjunt que diem N.

Així N = {1 , 2, 3, 4, 5, 6, …..1200, …}

• Normalment intentem establir sempre un ordre entre els nombres. Aquella quantitat és més gran que , jo tinc més anys que tu, etc.

Hi ha una notació estàndard per indicar que 17 és més gran que 12, per exemple.

Així 17 > 12 o també s’escriu 12 < 17.

Altres exemples :

a) 20 + 3 < 20 + 4

b) 24 monedes de 5 Ptes. donen una quantitat < 15 monedes de 100 Ptes.

• Podríem dir també que els naturals son la suma dels parells i dels imparells. Dit d’una altra manera {2, 4, 6, 8,….} més {1, 3, 5, 7, 9,….} ens dóna el conjunt de tots els naturals.

Fixat per exemple que fent 2*N + 1 , i agafant diferents valors de n, ens dona sempre un nombre senar (imparell).

N=3 2n+1 = 7

N=5 2n+1 = 11

….

Prova tu mateix de cercar altres imparells d’aquesta manera.

• Els nombres Parells també es diuen múltiples de 2 donat que s’obtenen multiplicant qualsevol nombre x 2.

En Matemàtiques per abreviar de vegades escriurem

• Els múltiples de 3 també tindrien una notació semblant. Així

{ 3, 6, 9, 12, 15, …. 30…}

ACTIVITAT_1.

Donat que 6 i Y 1000 Ptes. O dit d’una altra manera 5 i Y 500 Ptes. Podem aprofitar aquest fet per fer conversions aproximades d’una moneda a un altre.

Així per exemple un article que val 390 i , aquesta quantitat dividida entre 3 ens dona 130, llavors 130 x 500 = 65.000 que seria aproximadament el preu en Ptes.

Completa tu mateix emprant aquest raonament la taula de baix:

Article	Preu i	Preu Ptes.
Rentadora Cotxe Tabac Llibre Vídeo	493 12500 265 24 212

Múltiples i divisors.

De fet observem que la majoria de nombres naturals s’obtenen a partir de nombres més petits. Vegem uns exemples:

2 = 1+ 1

12 = 1+1+1+1+….12 vegades.

15 = és el resultat de sumar el nombre 5 exactament 3 vegades = 5 + 5 + 5

En definitiva, molts naturals són nombres compostos i per tant la majoria tindrà una descomposició. A nosaltres ens interessa la descomposició factorial. Consisteix en escriure el nombre com a producte de potències de nombres primers.

Així 12 = 3·2²

Els primers seran aquells nombres que no tenen divisors més que 1 i ells mateixos. Són primers els 3, 5, 7,13…31.

ACTIVITAT_2

Completa una taula dels 100 primers nombres com la de baix i ves taxant tots els nombres compostos fins que quedin només nombres primers.

..11	12	13	14	15	16
22	23	24	25	26	27 ..			..
..	..	..
92	93	94	95	96	97..			100

Criteris de divisibilitat.

A la pàgina 25 tens una taula dels criteris més coneguts per mirar quan un nombre és divisible per 2, 3, 5, 9 i per 11.

De tota manera, sempre queda el recurs de la calculadora. Un nombre és divisible per un altre quan el resultat de la divisió és sencer.

Però, per què ens interessa això dels múltiples i divisors ? Pensa en el següent exemple:

• La Marta és representant d’una marca comercial de begudes i ens diu que passarà pel nostre restaurant cada 6 dies. Avui som dia 5 de Març i el 2 d’abril tenim un sopar per 250 persones encomanat. Voldríem saber quin serà la ultima comanda que farem a la Marta abans del sopar.

Nota: Ahir mateix va passar la Marta i li vam encomanar 12-caixes de cervesa San Miquel i 3-barrils.

• Fem comptes :

4 + 6 = dia 10 de Març

10 + 6 = dia 16 …+6 = dia 22 de Març + 6 ..= dia 28 de Març. Quants dies té el Març?

• Els nombres primers han jugat un paper important al llarg de la història. A la actualitat s’empren per exemple per xifrar tot tipus de missatges digitals a les telecomunicacions, a les transaccions bancàries a través d’Internet. La clau de xifrat és de vegades el producte de nombres primers molt grans i els potents ordinadors necessiten molt temps per trobar-la.

Et proposem 2 activitats relacionades amb els nombres primers:

1) distribueix els nombres en forma d’espiral tal com veus al gràfic de baix .. Fes el gràfic tan gran com puguis. Fixat en el files, columnes i diagonals. Veuràs que estan plenes de nombres primers. Podríem dir que caminant en la direcció de certes diagonals trobes “filons” de primers.

2) Una manera de trobar nombres primers grans consisteix en fer p1·p2·p3·p4…+1 Els nombres p1,p2, p3…han d’ésser nombres primers consecutius i no n’has de deixar cap.

Així :

2·3 +1 = 7

2·3·5 +1 = 31

2·3·5·7 +1 = 211

Et proposem que trobis així al menys 4 nombres primers més grans que 1000.

• La descomposició factorial dels nombres és factible a ma quan no son molt grans. Et proposem que ho provis amb els nombres 16, 25, 48 i 60.

Així 36 = 2² · 3²

Múltiples i divisors.

La majoria de nombres tenen múltiples i divisors. Naturalment els primers no tenen divisors propis. En canvi, tots els nombres tenen múltiples, i de fet, tants com vulguem.

• M.C.D. ( 24, 6 ) = factors comuns d’exponent més baix = 3·2

• M.C.M. ( 7 , 15 ) = tots els factors amb exponent més gran = 7·3·5

• Et proposem que els cerquis pels nombres 420 i 148.

• De vegades no és senzill veure si un nombre té divisors. Fins i tot els ordinadors més potents necessiten temps per determinar si un nombre és primer. (Naturalment quan els nombres són grans)

De fet, a l’hora de provar divisors d’un nombre només cal que ho provem per aquells primers < que la seva arrel.

Per exemple, volem saber si el 323 és primer.

- Fem Ö323 » 17’97..

- Agafem tots els primers fins el 17: 2, 3, 5, 7, 11, 13, 17

- Si el nombre no és divisible per cap d’ells podem garantir que és primer.

• Et proposem que estudiïs tu mateix si son primers o no els nombres 211, 3943 i 923.

Activitats Clic.

El programa Clic ja fa temps que es distribueix als centres de Catalunya i Balears. Molta gent ha desenvolupat activitats i materials de quasi bé qualsevol àrea o tema que us pugeu imaginar.

• Us proposem aquí que completeu el paquet d’activitats anomenat “Divisibilitat” dins l’aula Informàtica del vostre Centre.

Calculadora.

Practica una mica els operadors +, ·, =, /, ( , … fet els exercicis proposats a la pàgina 41 del llibre de Matemàtiques 3ESO d’Anaya.

Exercicis 47, 48, 49, 51, 54 a)

Observa quantes xifres decimals mostra per pantalla jugant amb la seqüència

MODE FIX n

Exercicis.

1. Insereix el signe < (menor que) o > (major que) segons correspongui:

a) 12 15

b) 7 2

c) 93 101 d) 55 23

2. Troba tots els múltiples de 13 compresos entre el 400 i el 450.

Ex. 13 · 31 = 403

3. Troba tots els divisors de 150 dins els conjunt {1,2,3,4,…..14}

4. Situa els nombres 36, 218, 312, 3330, 216, 3000, 424, 2320 a la columna del divisor més gran que trobis.

2	3	4	5	6	9	10	100
						3330	3000

5. Dóna una definició de nombre primer. Quants n’hi ha ?

6. Calcula amb les regles vistes a l’aula el :

• M.c.d. ( 720, 440 )

• M.c.m. ( 66, 99 )

7. Dos ciclistes parteixen el mateix moment i donen voltes a una pista circular en el mateix sentit. Un d’ells tarda en donar una volta 6 min. I l’altre 8 min. Quant temps estaran en tornar-se a trobar? Quantes voltes haurà donat cadascun?

Nombres naturals i divisibilitat.

1. Ordena les següents sèries de nombres fent servir els símbols <, > :

a) 12, 15, 7

b) 8, 15 , 2

c) 93, 99, 9

2. Troba la descomposició factorial dels nombres proposats baix.

Ex. 91 = 7 ·13

a) 1224

b) 111

c) 1236

3. Cerca el m.c.d. i el m.c.m. dels nombres 720 i 440

4. Troba tots els divisors de 15 i 16. Podríem dir que no tenen divisors comuns ?

Quin és el m.c.m.?

5. Estudia si els nombres 133 i 421 són primers. Explica amb detall el procés que has seguit per saber-ho.

Ex: Per estudiar si el nombre 1327 és primer, fem Ö 1327 @ 36,42… i per tant provem tots els primers que trobem fins el 36.

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31

Comprova finalment el càlcul:

2² · 3 · 5 · 7 + 1 = 421

Els nombres enters.

Al llarg de la història l’home té la necessitat d’emprar nombres negatius. Tant per indicar el sentit del deute com per exemple el sentit de moviment al pla.

Vegem per exemple un típic gràfic de punts al pla emprant un sistema de coordenades:

Podríem dir que el zero neix també del fet d’afegir els nombres negatius:

1 + (-1) = 0

Els enters són el resultat de ajuntar tots els naturals, el zero i els negatius. Anomenem generalment Z aquest conjunt de nombres.

Z = { …..-4, -3, -2, -1, 0 } U { 1, 2, 3, 4, ….} = tots els enters.

Operacions.

Les operacions de sumar, restar i multiplicar enters són conegudes. Comentem breument 2 propietats importants : la associativa i la distributiva.

Suma +

Resta -

Producte · Els símbols que apareixen a la dreta seran els més emprats.

La suma i la resta, són de fet la mateixa operació, donat que per exemple :

3 – 5 = -2 La resta de 3 i 5 dona –2.

3 + (-5 ) = -2 La suma de 3 amb el negatiu –5 dóna –2.

Associativa.

2 + (3 + 5) = 2 + 8 = 10 dóna el mateix resultat si situem el parèntesis al principi.

( 2 + 3 ) + 5 = 5 + 5 = 10

Distributiva.

4·(3 + 5) = 4·3 + 4·5

(2 + 7 )· 3 = 2·3 + 7·3

• El model de l’esquerra val per qualsevol terna de nombres enters.

• Quan té sentit aplicar-la? De fet el cas més clar es quan intervé una variable a la operació aritmètica.

Ex: 3 ·( a + 1) = 3·a + 3

Fixat que ara no tenim un resultat numèric de la operació aritmètica fins que no donem un valor a la variable a

• De vegades l’apliquem per treure factor comú, quan per exemple un conjunt de nombres tenen el mateix divisor:

12 + 16 + 24 = 4· (3 + 4 + 6) = 4·13 = 52

Exercicis.

1. Fes els càlculs respectant l’ordre dels parèntesis i les propietats vistes a l’aula.

a) ( 5- 3 )·(7 – 4) + 2·( 3·(6 – 2) ) =

b) 9 – 2·3 =

c) (15 – 35)·(14 – 4) + 11 =

d) 2·8 + 4·[ 2 +3·(11-3) ] =

2. Calcula de 2-maneres diferents les operacions:

a) 7·(8 + 4) =

b) (6 +2 )·(4+5) =

c) ( 8 + 5 )·( 9 – 4 ) =

3. Aplica la propietat distributiva i agrupa els termes semblants.

a) 3·( 4 + 5x) =

b) (5 + a)·(2 + a) =

c) (3 + 2x )·( 4x + 1)=

4. Treu el factor comú convenient i calcula després el resultat.

a) 12 + 16 + 40 = 4· (3 + 4 + 10) = 4 · 17

b) 28 + 36 – 44 =

c) 2a + 5a + 12a =

d) 14x – 10x + 5x =

5. Comprova que si multipliques els 2 membres d’una desigualtat per un nombre positiu continua essent certa.

Ex: 7 > 4 Ara si multipliquem per 3 a cada membre obtenim:

21 > 12

Estudia tu mateix que passaria si multipliquem per un nombre negatiu. Posat tu mateix exemples com el de baix:

4 < 9 Però si multipliquem als 2-membres per (-1) , llavors - 4 < - 9 ?

6. Et proposem els exercicis de càlcul mental 13, 14 i 17 de la pàg. 38 del llibre Anaya. Aquells alumnes amb més dificultats poden fer només els més bàsics de la unitat didàctica.

Racionals, potències i decimals.

La unitat didàctica aprofundeix en els nombres, en les diferents notacions d’un mateix resultat numèric i també en l’ús de la calculadora amb els decimals, les potències i els nombres grans i petits.

Potències.

Recordem la definició quan l’exponent és enter, 2ⁿ =2·2·2...(n-vegades)

Exemples:

1. 2⁵ =2·2·2·2·2= 32

2. 3⁴ =3·3·3·3= 81

Quan la base és negativa (el nombre que cal elevar a un exponent) pot presentar problemes el signe del resultat. Vegem:

1. (-2)³ = (-2)· (-2)· (-2) = - 8

2. (-3)⁴ = (-3)· (-3)· (-3)· (-3) = 81

Fixat que el signe (+) o (-) del resultat dependrà del nombre de vegades que multipliquem la base. En general funciona la regla:

• Exponent parell = resultat (+)

• Exponent senar = resultat (-)

* Ara només cal resoldre 2-petits dubtes:

1. Què passa quan l’exponent és zero ?

2. I quan l’exponent és negatiu, quin sentit té ?

La primera pregunta té una resposta lògica, donat que a tot producte podem posar la unitat, aquest ha d’ésser el resultat.

La segona és conseqüència del fet que podem sumar exponents quan tenim la mateixa base. Vegem:

2³ · 2⁴ = (2·2·2·) · (2·2·2·2) = 2⁷

Llavors per coherència, per exemple 2² · 2^(-2) = 2 ^{(2 –2)} = 2⁰ . Si pensem una mica la potència negativa haurà d’ésser l’invers de 2². Resumint tot el que s’ha dit tenim les propietats de la pàg. 30 del llibre Matemàtiques 3ESO.

Propietats.

1. 2^m · 2ⁿ = 2^m+n Exemple: 2³ · 2⁴ = 2³⁺⁴ = 2⁷ = 128

2. (2^m)ⁿ = 2^m·n

3. 2⁰ =1

1. 2^-n = 1/2ⁿ

Si canvieu la base 2 per qualsevol altre nombre positiu les propietats també es compleixen. A la pàg. 30 s’ha canviat la base 2 per un nombre qualsevol a, positiu.

La calculadora disposa de la tecla x^y per calcular potències d’exponent sencer. Practica tu mateix amb alguns exemples senzills dels que ja coneguis els resultats.

Així 2⁵ = 2 x^y 5 = 32. Cal vigilar perquè els resultats poden ser grans quan augmentem l’exponent. Fixat en els càlculs que tens proposats en els exercicis de baix

Exercicis.

1. Practica una mica amb les potències.

a) Escriu en forma de potència 100, 1000, 0’000001

b) Escriu en forma de potència els nombres 32, 1024, ½ i 1/16.

c) Calcula 18³, 34⁶ i 3⁹⁸. Què en penses dels resultats ?

2. El càlcul 20.000.000 · ( 1 + 0’065 )¹⁰ ens calcula el capital final al cap de 10 anys d’una inversió de 20 milions col·locada al 6’5% de rendibilitat anual.

Podries fer un càlcul semblant per calcular el capital final al cap de 15 anys ?

3. Si l’IPC que ens indica la pujada dels preus en mitja durant un any econòmic es mantingués constant al llarg de 5 anys al voltant d’un 2’7%, tindríem:

1 cafè amb llet 175 Ptes. --> l’any vinent 175·(1’027) --> l’altra 175·(1’027)² ...

1 cervesa 225 Ptes. --> l’any vinent 225·(1’027) --> l’altra 225·(1’027)² ..

i així durant els 5 anys que l’IPC fora constant.

Podries calcular els preus d’aquests articles al cap de 5-anys ?

Gràfic.

• Típica gràfica de les potències senceres d’un nombre.

• Els exponents apareixen a l’eix OX.

• Els resultats de les diferents potències apareixen en notació mantissa + exponent donat que els resultats aviat són força grans.

Els racionals.

Els grecs ja els empraven com a quocients de longituds senceres. Els nombres 1/3, 2/5, 3/7...etc. eren habituals en els seus càlculs.

Podríem classificar els racionals en 2 tipus ben diferenciats:

• FINITS 5/2 = 2’5 .

On la part decimal és finita.

• PERIÒDICS 1/3 = 0’333333

On la part decimal és periòdica (es repeteix indefinidament ).

Esbrina tu mateix si son finits o periòdics els nombres 2/6, 12/7, 23/8 i 45/4.

Naturalment sempre els podem escriure en forma de fracció o bé en la seva forma decimal. Vegem uns exemples:

3’428571..428571..etc. = 24/7

12’2 = 61/5

Fracció generatriu.

Per obtenir la forma decimal només cal fer la divisió amb la calculadora. Passar de la forma decimal a la forma de fracció ja no es tan directe, cal conèixer un parell de regles:

PERIÒDICS PURS -->

(Totes les xifres – part sencera) / 999..(tants com xifres periòdiques)

PERIÒDICS MIXTES -->

(Totes les xifres – part no periòdica)/ 99..(xifres periòdiques)00..(no periòdiques)

3’23..23..23 = (323 – 3) / 99 = 320/99

5’2344444... = (5234 – 523) / 900 = 4711/900

Operacions.

Els racionals són un conjunt tancat si emprem les operacions bàsiques + , · i divisió. Repassem una mica com operem amb les racionals.

± Cal agafar fraccions equivalents amb el mateix denominador.

½ - 1/3 = 3/6 - 2/6 = (3 –2 )/6 = 1/6

· Multipliquem numeradors i denominadors i expressem el resultat també en forma de quocient.

½ · (-1/3) = 1·(-1) / 2·3 = -1/6

(-2/5)·(2/3) = (-2)·(2)/(5)·(3) = -4/15

: Multipliquem per la fracció inversa.

2/7 : -1/3 = 2/7 · (-3/1) = (2)·(-3) / (7)·(1) = -6/7

Exercicis.

1. Reflexiona el problema de la pàgina 22 del llibre Anaya.

2. Fes un exercici semblant als de la pàgina 28. Per exemple:

2/5 – 1/3 · (2 – 1/5) – 3·(2/7)

3. Fes els exercicis 1, 2 i 4 de la pàgina 38 del llibre de 3^er Eso Anaya.

4. Fes els 7, 8 i 10 de la pàgina 38 del llibre de 3^er Eso Anaya.

Notació científica.

La calculadora empra també la notació científica per nombres molt grans o petits. Fixeu-vos que en aquests nombres el nombre de xifres decimals de vegades és gran i per tant hi ha un error també en aquesta notació. Vegem alguns exemples.

a) Així 50.000.000 = 5 x 10⁷ . La calculadora ens mostra 5 ⁷

b) 318.978.453 = 3’18978453 x 10⁸ . La calculadora ens mostra 3’18978453 ⁸

5. Fes l’activitat 1 de la pàgina 31 del llibre Anaya.

6. Consulta la taula de la pàg. 25 on hi ha alguns prefixos emprats a les unitats de mesura de pes, longitud, temps ...etc.

• Què es un microsegon ?

• Si la unitat megaeuro fora implantada al mercat, a quants euros equivaldria?

7. Fes els exercicis 16, 17 de la pàgina 36 del llibre Anaya.

Exercicis.

8. Fes els exercicis 19, 20 i 21 de la pàgina 39 del llibre de 3^er Eso Anaya.

9. Fes els exercicis 22, 23 i 25 de la pàgina 38 del llibre de 3^er Eso Anaya.

10. El 28 de la pàgina 38 del llibre de 3^er Eso Anaya.

2. Proporcionalitat, percentatges, i repartiments.

Moltes situacions pràctiques ens obliguen a emprar raons i proporcions, en definitiva els nombres racionals que ja coneixem.

A un quocient de dos enters a, b del tipus de baix, li diem també raó.

Així també una proporció és una igualtat entre dos nombres racionals o raons.

Quan dues magnituds són proporcionals sempre és possible trobar el valor de l’altre coneguts dos valors de la primera magnitud.

Exemple: És clar que les alçades d’en Francesc i na Maria són proporcionals a les seves ombres i per tant:

;

Si suposem conegudes les altures 1,62 m. i 1,58 m. juntament amb l’ombra d’en Francesc 1,78 m., llavors podem calcular fàcilment l’ombra de na Maria:

à à

Recordem també que dues magnituds són directament proporcionals quan en augmentar una (doble, triple ) també augmenta l’altra en la mateixa proporció (doble, triple )

Per exemple, si l’alçada d’un objecte és doble que un altre, la seva ombra també serà el doble.

Podríem dir també que en aquelles situacions on hi ha proporcionalitat directa podem aplicar la coneguda “regla de tres”.

Exemple: Si per transportar 120.000 l. D’aigua necessitem 8 camions, quants fan falta per transportar 315.000 l.?

120.000 l. ----------- 8 camions

315.000 l. ----------- x

En els problemes de proporcionalitat composta, es a dir on intervenen més de dues variables o magnituds, convé fer-ne una reducció a la unitat. Vegem un exemple:

Per encalentir 100 gr. D’aigua des de la temperatura ambient de 17º fins a 80º necessitem 1.785 calories.

calories necessaries per pujar un grau de temperatura.

calories necessaries per pujar 1º de temperatura 1 gr. d’aigua.

En els repartiments proporcionals, només cal recordar que les parts, a més de proporcionals, cal que ens donin la unitat.

Per exemple: Si volem repartir beneficis de 2.500.000 € entre els directius d’una empresa proporcionalment als seus nivells de formació 24, 12 i 8 respectivament, només cal fer 24 + 12 + 8 = 44 parts.

Llavors a cadascun li tocarien 24, 12 i 8 parts respectivament:

és la quantitat que ara cal multiplicar per 24, 12 i 8.

x 24 = 1.363.636 €

x 12 = 681.818 €

x 8 = 454.546 €

Activitats.

1. Al llibre de 3ESO hi ha molts exemples per fer, comença per els de les pàgines 50 i 51.

2. Fes almenys dos exemples de les pàgines 52 i 53 del llibre.

3. Fes els 8, 12, i 15 de la pàgina 60 del llibre Matem 3ESO Anaya.

4. Fes els 17, 19, 22 i 26 de la pàgina 61.

Percentatges.

Moltes situacions de la vida quotidiana ens obliguen a emprar percentatges, ja sigui en forma de tant/unitat o be en forma de %. Vegem algunes situacions:

1. El Banc ens diu que ens cobrarà un interès d’un 8’5% al préstec que hem fet per pagar el cotxe. Amb altres paraules de cada 100 Ptes. que ens deixen, 8’5 Ptes. se les queda el Banc.

2. El constructor de la nostra casa ens diu que normalment té un benefici industrial del 10%. Traduït en Ptes. això vol dir que després de calcular els materials, els sous del manobres, el terreny i permisos corresponents cal afegir el 10%.

• De fet, ens adonarem que per calcular el preu final d’un article, només cal multiplicar per un factor convenient del tipus (1 + r/100)

On r és el % d’augment sobre el preu inicial.

• Als descomptes, la situació és semblant, però ara multipliquem per (1 - r/100)

On r és el % de descompte sobre el preu inicial.

• Cal vigilar amb els % perquè no son lineals. Vegem 2 exemples :

- No és el mateix una puja de sou d’un 5% que aplicar una puja d’un 3% el Febrer i una altra d’un 2% el Setembre.

- Si un comerciant ha baixat els preus el gener un 20% no els aconseguirà deixar igual amb una puja d’un 20% el mes de maig.

Intenta resoldre tu mateix les situacions següents:

1. Un comerciant compra objectes per valor de 90.000 Ptes. Les despeses de transport li suposen el 6% del preu de la compra. Quant haurà de pagar en total ?

2. Un producte que pesa 150 grams té el 15% del component A, el 30% de B, el 20% de C i la resta del component D. Quina quantitat en gr. Hi ha de cada component ?

3. Un recipient conté 78 Kg. d’aigua salada. El 2% d’aquesta és sal. Quina quantitat hi ha d’aigua i de sal respectivament ?

4. D’un poble de 20.000 persones, el 32% duen ulleres i d’aquestes, el 45% són dones. Quantes dones amb ulleres hi ha ?

5. Un moble m’ha costat 6.000 Ptes. A quin preu l’he de vendre per guanyar el 20% ?

6. Augmenta les següents quantitats:

34.900 en un 15% .................

500.000 en un 0’5% ...............

17.800 en un 85% .................

2.500 en un 100% .................

7. A un hipermercat hi ha rebaixes. Calcula el preu que haurem de pagar per cada producte, aplicant el descompte indicat en cada cas :

camisa 7.500 Ptes. , un 15% .................... Preu rebaixat..........

televisió 89.900 Ptes., un 12% .................... Preu rebaixat..........

corbata 2.500 Ptes., un 21% .................... Preu rebaixat..........

8. Un producte valia 2.300 Ptes. i he pagat 1.600 Ptes. Quin % de descompte m’han fet ?

9. Fes les activitats de la pàg. 55 del llibre de 3^er ESO.

10. Consulta l’exercici resolt de la pàg. 56 del llibre de 3^er ESO.

11. Fes les activitats de la pàg. 56 del llibre de 3^er ESO.

Interès compost.

Es tracta en definitiva d’un encadenament de percentatges on es manté constant el % que apliquem diverses vegades.

Exemple: Si apliquem un 5% d’augment a una quantitat de 5000 € de forma reiterada 4 vegades, tenim el de baix.

€

Consulta tu mateix els exercicis resolts de la pàg. 58 del llibre.

Activitats.

12. Fes les de la pàg. 57 del llibre de 3ESO.

13. Fes també les de la pàg. 58 del llibre de 3ESO.

14. Fes els 34, 38, 40, 44 i 47 pàg. 62 del llibre de 3ESO.

15. Fes l’exercici 51 de la pàg. 63 del llibre de 3ESO.

3. Sèries Numèriques. Progressions

Reflexiona una mica l’exemple de la pàg. 66 del llibre Mat 3ESO d’Anaya. Naturalment t’hauràs d’ajudar de la calculadora per fer càlculs del tipus:

2 SHIFT X 22 = 4.194.304 !

Algunes permeten calcular la suma dels seus primers 100, 200,..340 termes. Diem que tenim una sèrie quan la seqüència de nombres segueixen certa regla, per exemple:

5, 10, 15, …. 75

Fixa’t que el que fem és repetir certa operació sobre el darrer terme de la sèrie que anem calculant.

Aritmètiques.

Sumem sempre una quantitat constant al darrer terme.

Geomètriques.

Multipliquem per una quantitat constant o raó el darrer terme.

1, 2, 4, 8, 16, 32, 64, …. ( creixen ràpidament quan la raó és significativament més

gran que la unitat )

De fet, l’interès compost que ja hem estudiat anteriorment és un exemple clar de progressió geomètrica.

Activitats.

1. Reflexiona l’exemple de les cartes de la pàgina 70 del llibre. No es gens immediat !

2. Fes també tres activitats de la pàg. 70 del llibre de 3ESO.

3. Comprova que els 50 primers parells dins el conjunt {1,2,… 100} sumen 50 unitats més que els senars.

Nota: Obtén primer la suma 1 + 2 + 3 + 4 +… 100 = parells + senars.

4. Fes les activitats 2 i 5 de la pàg. 73 del llibre de 3ESO.

Suma de termes d’una progressió.

A la pàgina 74 del llibre està ben explicat el cas més interessant, els termes d’una progressió geomètrica.

Quan la raó de la progressió és més gran que la unitat, va be emprar la fórmula en la forma que apareix baix.

Per exemple, a la mateixa pàgina sumem els termes 3+6+12+24+…384 ( es a dir 8 termes d’una progressió on r = 2 )

= = 3 · ( 256 – 1) = 765

En canvi, quan la raó és més petita que la unitat, convé emprar la fórmula amb un canvi de signe al numerador i denominador.

=

Vegem un exemple, voldríem sumar , que és el mateix que sumar 21 termes en progressió on r = ½

= = 1,9999998..

Activitats.

4. Fes les activitats de la pàgina 76 del llibre. A la mateixa pàgina explica que de fet l’interès compost és també una progressió geomètrica.

5. També és interessant el cas de sumar un nombre molt gran de termes quan aquests es fan molt petits, es a dir r < 1

Llavors, podem suposar que quan n és molt gran. Així és possible sumar un nombre infinit de termes:

6. Fes els exercicis 2, 5 i 8 de la pàgina 78 del llibre de Matemàtiques 3ESO Anaya.

7. Fes almenys 4 exercicis de la pàgina 79.

4. Llenguatge algebraic. Polinomis

Les expressions amb una variable apareixen contínuament a la resolució de problemes. Les expressions del tipus x + 2, x² –3x , són expressions algebraiques que no tenen ara un resultat numèric fins que no assignem un valor arbitrari a la variable x.

Moltes vegades anunciats del tipus “la meva edat era doble que la teva l’any passat” tenen la seva corresponent expressió algebraica.

• Fixat en els enunciats de la pàgina 86. Els comentes amb el teu mestre.

• Resol tu mateix els plantejaments de la mateixa pàgina.

• Fes també totes les activitats proposades a la pàgina 87 del llibre Anaya.

• Observa també les definicions de monomi, polinomi, identitat i equació de la pàgina 88 del llibre. Posa tu mateix un exemple diferent dels proposats a la mateixa pàgina de cadascuna de les expressions.

Monomis.

Diem monomis al producte de una o varies variables per nombres reals. Per exemple : 2x , 2xy, 5a² ... són monomis.

Polinomis.

Diem polinomi amb una variable, a la suma i resta d’un nombre qualsevol de monomis amb la mateixa variable.

Així, per exemple:

X² – 3x + 1

X³ –4x² –3 , 2x² – 3x , ... són polinomis en la variable x.

Grau.

És l’exponent més gran en que apareix la variable del polinomi.

Operacions.

Així com els nombres es poden sumar, multiplicar i dividir, els polinomis també. En general agruparem els termes semblants (del mateix grau) com els exemples:

• 2x –3 + 4x = 6x –3

• x² –4x + 7 –2x² = -x² – 4x +7

Als productes, per exemple, només cal aplicar la propietat distributiva:

• (2x –1 ) · (x² –3x ) = 2x³ –6x² –x² +3x = 2x³ –7x² +3x

Queda clar també que tot polinomi te la seva forma reduïda, com a l’exemple:

• -x³ –3x² + 2x³ –4x +2 = x³ –3x² –4x +2 que resulta d’agrupar termes semblants.

Activitats.

Fes les proposades a la pàgina 89 del llibre de 3r ESO.

Valor numèric.

Naturalment un polinomi no és més que una expressió algebraica que depèn d’una variable i per tant no té sentit demanar un resultat numèric.

De tota manera, si escollim un valor per la variable, llavors el polinomi defineix clarament una operació aritmètica que podem calcular. El seu resultat rep el nom de valor numèric del polinomi.

Vegem uns exemples:

X² – 3x + 7 és un polinomi que pot prendre infinits valors i que depèn del valor de x.

Llavors (1)2 – 3(1) + 7 = 5 és el valor numèric del polinomi quan x =1.

2x³ – 3x – 6 és un polinomi de grau 3 que pot prendre infinits valors i que depèn de x.

Llavors 2·(-1)3 – 3(-1)- 6=- 5 és el valor numèric del polinomi quan x = -1.

Arrels d’un polinomi.

Quan un valor de la variable anul·la el polinomi, parlem d’una arrel o zero del polinomi.

• Per exemple : 3x – 6 té només un zero, x = 2.

La majoria de polinomis tenen zeros, de fet els polinomis que no en tenen s’anomenen primers. ( semblant als nombres primers que no descomponen en producte de factors )

Per exemple: x² –3x + 7 no té zeros reals. És un polinomi primer.

El Quadrat del binomi.

Aquesta i altres identitats s’empren contínuament al llenguatge algebraic. De fet totes son el resultat d’aplicar correctament la propietat distributiva.

Les teniu a la pàgina 92 del llibre de 3^r ESO.

Vegem però ara uns exemples de la seva aplicació :

• ( a +1 ) ² = a² +2a + 1

• ( 2x - 1 )2 = ( 2x – 1 )·( 2x – 1 ) = 4x² – 4x + 1

• ( 3x + 2 )·( 3x – 2 ) = 9x² - 4

• i al revés també, hi ha polinomis que poden expressar-se com un quadrat.

4x² + 4x + 1 = ( 2x + 1 )²

Activitats.

1. Fes almenys 3 apartats de les proposades a la pàgina 90 del llibre de 3r ESO.

2. Fes almenys 4 apartats de les proposades a la pàgina 91.

3. Observa les identitats de la pàgina 92. Fes les activitats proposades a la mateixa pàgina.

4. Fes les activitats 3, 5, 7, 9, 12 i 14 b) c) de la pàgina 93.

Fraccions algebraiques.

Són senzillament quocients de polinomis com els exemples de baix.

;

Algunes fraccions algebraiques admeten de vegades formes més simples, sobretot quan trobem monomis del mateix grau al numerador i denominador. Vegem uns exemples:

Activitats.

1. Fes les activitats 1, 3 i 4 de la pàgina 95 del llibre de 3^r ESO.

2. Fes els exercicis de la unitat 3, 4, i 5.

3. Fes almenys 2 apartats de cadascun dels exercicis de les pàgines 98 i 99 del llibre.

4. Fes també el 39 i 40 de la pàgina 101 del llibre de 3^r ESO.

5. Per acabar, dels problemes d’estratègia del final de la unitat seleccionem el 1 i el 5 de la pàgina 102 i també el 3 per a pensar de la pàgina 103 del llibre.

Aplicacions.

Escriure en forma algebraica té moltes aplicacions, en la resolució de problemes, en l’establiment de fórmules que calculen conceptes quotidians com el canvi de moneda, l’interès compost, .. etc.

Vegem una aplicació senzilla. Intenta simplificar l’expressió algebraica a² – (a+1)(a-1)

Sabem així automàticament els resultats de :

5² - 6·4 =

89² – 90·88 =

.

.

i així, per molt grans que siguin els nombres 88888² – 88889·88887 = a la unitat.

5.Equacions (1 variable).

Un dels aspectes que caracteritzen les matemàtiques és el fet d’emprar contínuament equacions. De fet, el que interessa més moltes vegades és saber si tenen solució.

A la pàgina 105 del llibre de 3r ESO tens un munt d’exemples d’equacions. D’altra banda, no et desanimis, donat que algunes equacions que veurem dins el curs malauradament no tindran solució.

Diem equació a tota expressió aritmètica amb 2-membres separats per un signe =, i que conté una quantitat desconeguda, que anomenem variable.

Ex:

Solucions d'una equació.

x³ -2x² + 2x-4 = 0 és una equació de tercer grau completa perquè en el polinomi ordenat del primer membre no hi falta cap monomi.

2 és una solució de l'equació perquè 2³-2(2)² + 2(2) - 4 = 0

1 no és solució d'aquesta equació perquè

(1)³ -2(1)² + 2(1) - 4 = -3 ¹ 0

Equivalència d'equacions.

Direm que dues equacions són equivalents si tenen

les mateixes solucions.

Exemple:

Les equacions 3x + 9 = 0 i 7x + 21 = 0

són equivalents ja que x = - 3 es la solució per a les dues

En general:

Dues equacions són equivalents si tenen les mateixes solucions (normalment podem obtenir l'altra equació multiplicant la primera per un nombre real)

Tipus.

Hi ha molts tipus d’equacions, la majoria de les que veurem durant el curs s’ajusten als diferents models que tens a la pàgina 100 del llibre de 3^r ESO d’Anaya.

Polinòmiques.

Del tipus 3·( x-5 ) – 2x + ( x-3 )/2 = 1.

La majoria tenen solució, moltes vegades tantes com el grau del polinomi que hi apareix a un dels membres.

Radicals.

La variable apareix dins el signe Ö , com l’exemple de baix:

Generalment n’hi ha prou amb aïllar els termes radicals i desprès elevant al quadrat els dos membres per arribar a una equació polinòmica.

--> -->

arribem així a una equació polinòmica de 2n grau.

Equacions de 1r grau.

Quan tenen solució, aquesta és sempre única i convindrà comprovar-la en la majoria de casos. La variable apareix amb exponent 1 i per tant són les més senzilles.

Vegem un exemple:

3x + 5 = 8 Clarament només hi ha un valor de x = 1 que compleix la igualtat.

• A les equacions amb denominadors convindrà multiplicar els 2 membres per el m.c.m. dels denominadors que hi apareixen. Exemple:

--> --> 6x –2x - 4 = 15

Activitats.

1. Fes les proposades a la pàgina 106 del llibre de 3^r ESO d’Anaya.

2. Fes almenys 5 apartats de les proposades a la pàgina 108 del llibre de 3^r ESO d’Anaya.

3. Dels exercicis de la unitat de la pàgina 114 del llibre, fes almenys 3 apartats dels nombres 1, 3 i 7.

François Viète

(1540-1603)

Més conegut pel seu nom llatinitzat, Franciscus Vieta va néixer a Fontenay-le- Comte. Va ser conseller del Parlament de Bretanya i durant el regnat d'Enric III i d'Enric IV.

Pot ser considerat el fundador de l'àlgebra moderna, va estudiar els treballs de Cardan, Tartaglia, Bombelli, Stevin i Diofant els quals li inspiraren la idea de fer servir lletres. Si bé ja amb anterioritat Euclides, Aristòtil i d'altres havien fet servir lletres en lloc de nombres específics, aquest ús era infreqüent, esporàdic i accidental.

Vieta va ser el primer a fer-les servir sistemàticament, no tan sols a incògnites sinó també com a coeficients.

Va estudiar les equacions i els mètodes per a l'extracció d'arrels, va calcular el nombre p amb una gran exactitud, va analitzar les funcions angulars, la trigonometria i la resolució de triangles.

Va morir a Paris el 1603; les seves Opera Mathematica foren editades per F. van Schooten a Lió I'any 1646.

Equació de 2ⁿ grau.

Ja hem parlat abans de Vieta, Cardano i altres matemàtics que resolen aquests tipus d’equacions amb una fórmula que depèn dels coeficients del polinomi que intervé a l’equació.

Exemple:

x² – 3x + 2 = 0

Cardano per exemple, ja aplicà la fórmula x = = Que ens dóna les solucions 2 i 1 per la variable x.

Fem però ara tres observacions :

• Els valors 1 i 2 són arrels del Polinomi x² – 3x + 2.

• El producte ( x – 1 )·( x –2 ) = x² – 3x + 2. Dit d’una altra manera, quan un polinomi té arrels, té també una descomposició en forma de producte de polinomis més simples.

• Una equació del tipus de dalt no tindrà sempre solució. Ja que el terme dins l’arrel pot ser negatiu. Exemple : x² – x + 2 = 0 no té solucions reals.

Activitats.

1. Determina si les equacions de la pàgina 109 del llibre de 3^r ESO d’Anaya tenen o no tenen solucions.

2. Resol les equacions de la pàgina 110 del llibre.

3. Fes les activitats de la pàgina 111 del llibre de 3^r ESO d’Anaya

Fórmules de Vieta.

Moltes vegades convindrà emprar la forma normalitzada de l’equació, per exemple:

(1) 3x² – 6x + 12 = 0 és una equació equivalent a :

(2) x² – 2x + 4 = 0 on el terme x² està multiplicat per la unitat.

Llavors, les solucions de l'equació (2) x₁,x₂ compleixen :

x₁ + x₂ = -b

x₁. x₂ = c

Les igualtats anteriors permeten moltes vegades trobar les solucions senceres d’una equació sense haver d’aplicar la fórmula de Cardano vista anteriorment.

Exemples:

x² – x –2 = 0 Té solucions x = -1 i x = 2.

x² – 9x + 14 = 0 Té solucions x = 2 i x = 7.

Pots trobar tu les solucions ?

Nota: Les possibles solucions senceres de l'equació (2) han d'ésser divisors del terme independent c.

Resolució de Problemes.

Plantejar una equació a partir d’un enunciat d’un problema consisteix en traduir a llenguatge algebraic les condicions que uneixen allò que sabem amb allò que desitgem conèixer.

Podríem resumir-ho amb les passes següents:

1. Identifiquem les dades conegudes i donem nom a la variable.

2. Relacionem mitjançant una igualtat (equació) allò conegut amb allò desconegut (dit també variable).

3. Resolem l’equació amb algun dels mètodes estudiats.

4. Interpretem la solució i l’ajustem a l’enunciat.

Activitats.

1. Fes les proposades a la pàgina 112 del llibre de 3^r ESO d’Anaya.

2. Fes almenys 3 apartats dels exercicis 8, 10 i 11 de la pàgina 115 del llibre.

3. Dels exercicis de la unitat de la pàgina 116 del llibre, fes almenys el 16, 18, 20, 26 i 29 per completar la teoria.

Regla de Ruffini.

Consisteix en la divisió d'un polinomi P(x) per (x-a) utilitzant només els coeficients del polinomi.

D'altra banda, si el resta de la divisió anterior és zero, tenim que (x-a) és un factor primer del polinomi, ó el que és el mateix el valor a és un zero del polinomi.

Ex: Volem resoldre l'equació 3x² -4x +1 = 0

Intentem la divisió del polinomi per (x-1) amb la regla de Ruffini:

3 -4 1

1 ____3__-1__

3 -1 0 ==> resta

Tenim així el polinomi factoritzat : (x-1)(3x-1) i per tant també les solucions de l'equació anterior x = 1 , 1/3

Exercicis.

Utilitzar la regla de Ruffini per descompondre i resoldre les equacions:

x³ -2x² -5x +6 = 0

2x³ +3x² -8x +3 = 0

x³ +2x² -5x -6 = 0 * Recorda que si hi ha solucions senceres han d'ésser

divisors del terme independent del polinomi.

Equacions Irracionals.

De vegades, en la resolució d'un problema certa variable (objectiu a calcular) ens apareix dins una arrel ( ja sigui quadrada, cúbica, ..) Aquest tipus d'equació que apareix rep el nom de IRRACIONAL.

Ex:

* recorda que els resultats numèrics de les arrels són moltes vegades irracionals

Exercicis :

1. Empra algun mètode sistemàtic per resoldre les equacions de l’exercici 53 de la pàgina 115 del llibre.

2. Fes els apartats a), b) i c) del 51 de la mateixa pàgina.

3. Fes al menys 4 Problemes de les pàgines 112 i 113 del llibre de 3r ESO.

Sistemes d’equacions.

De vegades, el plantejament d’un problema, d’una situació geomètrica o de qualsevol qüestió numèrica requereix l’ús de dues o més equacions.

Nosaltres ens dedicarem als casos més simples: Situacions en les que intervenen

2 variables i les equacions lineals corresponents.

Exemple:

x + y = 5

2x – y = 7

En tots els casos semblants podem ésser sistemàtics i utilitzar un dels mètodes clàssics per trobar les variables x,y.

Cal fer però les observacions següents:

• Cadascuna de les equacions correspon a una recta del pla.

• De vegades el sistema no té solució, donat que les rectes corresponents són paral·leles. Exemple:

x+ y = 5

2x + 2y = -1

• Els casos que tenen solució, aquesta és única. Correspon al punt d’intersecció de les rectes.

• En els sistemes amb denominadors, procurarem primer convertir-los a un sistema equivalent sense denominadors.

@ és equivalent a

Activitats.

1. Fes les proposades a les pàgines 122 i 123 del llibre de 3r ESO.

2. Fes els apartats a), b) i c) del 51 de la mateixa pàgina.

3. Fes al menys 4 Problemes de les pàgines 112 i 113 del llibre de 3r ESO.

4. Els exercicis 2, 3, 5 i 6 de la pàgina 131 del llibre.

5. Els exercicis 31, 34 i 38 de la pàgina 134 del llibre de 3r ESO.

6. Els problemes geomètrics de la pàgina 135 del llibre de 3r ESO.

10. Estudi de funcions.

La variació de la temperatura al llarg de les hores del dia, el volum d’una esfera segons el radi que agafem, la variació del IPC al llarg dels mesos de l’any... són diferents exemples de funcions.

En aquest curs estudiarem només el cas d’una variable que depèn d’una altra variable que en diem independent.

Podríem dir que una funció pot venir donada de diferents maneres:

• Un enunciat que descriu com es relacionen les variables. Exemple:

La pressió en atm. augmenta dins l’aigua a mesura que ens anem endinsant de manera proporcional a la profunditat en que es trobem (en m.)

• Una gràfica o be una taula de valors on apareix clarament una variable sobre l’eix OX i l’altra sobre l’eix OY, juntament amb diferents valors (o punts de la gràfica).

• Una expressió aritmètica que relaciona clarament les dues variables. Exemple:

y = 3·x + 2

Variacions d’una funció.

Bàsicament es tracta d’estudiar com varia la variable y quan anem augmentant el valor de la X.( variable independent )

Observa els exemples de les pàgines 214 i 215 del llibre i a continuació estudiarem uns altres on la funció ve donada per una expressió.

1. y = 3x – 2

• Fes una taula de valors que contingui almenys 5 punts i la representació gràfica de la funció. Observaràs que naturalment estan alineats donat que una expressió de 1r grau en la variable independent és sempre una recta.

• Podríem dir en aquest primer exemple que la funció sempre creix donat que a mesura que agafem valors més grans de x la variable y també augmenta.

2. y = -2x + 4

• Fes el mateix que l’exemple anterior.

• Observa que ara la funció decreix donat que a mesura que augmentem la x l’altra variable y ara disminueix.

Naturalment, no tots els models són tan simples, només que augmentem una mica el grau del polinomi la gràfica té intervals de creixement i també intervals de decreixement.

3. y = -x² + 3x - 2

• Fes ara el mateix que als exemples anteriors. ( ara els punts no estan alineats, descriuen una paràbola )

• Podríem dir que la funció creix fins que agafem el valor per a x, en canvi quan agafem valors més grans, la funció decreix ( donat que els corresponents valors de y cada volta són més petits )

• Podríem dir també que al valor de x=3/2 hi ha un màxim de la funció. Observa que no hi ha altres valors de x que donin un valor més gran per a y.

De fet de funcions n’hi ha de molts tipus i el seu estudi de vegades depèn de la importància del model ( per exemple si afecta a una gran quantitat de gent, si explica el comportament de coses que considerem fonamentals com per exemple el moviment dels planetes al voltant del Sol, ...)

Funcions periòdiques.

Hi ha funcions periòdiques. Vol dir que basta conèixer la seva gràfica parcialment donat que es repeteix indefinidament. Les més conegudes i emprades, les trigonomètriques.

Exemple:

Si mesurem amb una camera fotogràfica d’alta velocitat l’alçada d’un pèndol sense arrossegaments quan oscil·la indefinidament en diferents moments obtindríem una gràfica aproximada a la de baix:

Activitats.

• Fes les proposades a la pàgina 217 del llibre.

• Observa també la gràfica de la pàgina anterior del vol d'una àguila, aquesta té uns mínims molt marcats. A quins valors del temps ?

• Fixat també que és impossible establir un model matemàtic exacte que ens permet fer prediccions.

Creixement i decreixement de funcions.

De vegades les funcions presenten trams on la funció creix ( en augmentar la variable x també augmenta la y ) i també trams on la funció decreix ( en augmentar la x la variable y disminueix ).

Observa per exemple la gràfica de pressió atmosfèrica de la pàgina 218 del llibre. La pressió per exemple augmenta durant els tres primers dies de la quinzena observada.

Quan en canvi una funció sempre creix o be sempre decreix en diem monòtona.

( creixent o decreixent )

Un exemple prou clar és la gràfica de pressió submarina de la pàgina 218.

• Dibuixa la recta que té per expressió y = 3x – 2 i comprova tu mateix que és monòtona creixent.

Diem també que una funció té un màxim en un punt quan el valor de la variable y és el més gran dels punts que l’envolten.

Diem que té un mínim en un punt quan el valor de la variable y és el més petit dels punts que l’envolten.

Observa alguna gràfica del llibre que té un mínim i veuràs que la funció decreix a l’esquerra d’aquest punt i en canvi creix a la dreta d’aquest punt. Per exemple la gràfica de temperatures de la pàg. 219

Activitats.

• Fes les proposades a la pàgina 220 del llibre Matemàtiques Anaya 3ESO.

Funcions contínues.

La majoria de funcions que observarem són contínues, es a dir la seva gràfica no se romp. De fet podem dir també d’una altra manera que les seves gràfiques no presenten “salts”.

Els “salts” que presenten les funcions que no són contínues s’anomenen també discontinuïtats de la funció. Un exemple d’aquest tipus el tens a la pàgina 221, veuràs una gràfica escalonada que representa el cost d’una cridada telefònica en funció del temps que ocupem la línia.

Naturalment hi ha també moltes funcions que presenten discontinuïtats, de vegades fins i tot els “salts” són infinits.

Prova tu mateix de fer una gràfica aproximada del model que tens a la taula de valors donada per:

x
-4	-1/4
-2	-1/2
-1	-1
0	??
1	1
2	½
4	...

Activitats.

1. Fes dues pràctiques de la pàg. 225 del llibre.

2. Fes les activitats 5, 6, i 7 de la pàgina 226 del llibre. Observes alguna funció discontínua ?

3. Per acabar, quina és la longitud aproximada del període de la gràfica de la funció trigonomètrica que observes a continuació ?

Expressió aritmètica.

El cas ideal en matemàtiques és quan tenim l’expressió que ens relaciona les dues variables.

Intenta seguir el següent exemple:

• Agafem un nombre qualsevol x dins l’interval [ 0 , 10 ]

• Agafem el seu complementari fins a 10, és a dir 10 – x

• Observem ara com varia el producte dels dos nombres :

• Construeix una taula de valors sencers del model emprant l’expressió anterior. Anomenem y al producte dels dos nombres ( que depèn del primer nombre que agafem x )

• Observa ara la gràfica obtinguda. Veus algun màxim a la gràfica ?

• Observes també que el producte creix a mesura que ens apropem al valor x=5 ?

• La funció té ara una expressió aritmètica que relaciona les variables x i el producte de x amb el seu complementari.

• Si agafem qualsevol altre interval, per exemple [ 0, 20 ], quin seria trobes el producte màxim observat ?

Altres funcions que tenen la seva expressió aritmètica les trobaríem a:

• la que relaciona l’àrea d’un quadrat amb la longitud del seu costat.

• L’àrea d’un cercle en funció de la longitud del seu radi.

• El volum d'una capsa construïda amb una cartolina de dimensions 30 x 40 cm. com la de la figura de la pàgina 222 del llibre. Observa també el gràfic de la mateixa pàgina. Observa el màxim de la gràfica, el valor de x corresponent és calculable ?

• L’àrea d’un triangle equilàter en funció del seu costat.

Àrea triangle =

De fet, aquest darrer model dóna un creixement de l’àrea molt semblant al model de creixement de l’àrea d’un quadrat.

11. Funcions Lineals.

És segurament el tipus de funció més senzill. La seva gràfica a tots els exemples que veurem a continuació és sempre una recta.

Reflexiona l'exemple de la pàgina 232 del llibre i fes les activitats que s'hi proposen al teu quadern personal.

Acaba tu mateix les rectes del gràfic i veuràs el punt de tall, moment en que convé fer-se soci del club de vídeo.

Def.

Dues magnituds són proporcionals quan els valors d'una s'obtenen a partir dels corresponents valors de l'altra multiplicant per un coeficient ( denominat constant de proporcionalitat ).

Contesta tu mateix les qüestions de la pàgina 233 del llibre i fes les anotacions corresponents al teu quadern.

La funció que relaciona dues magnituds proporcionals es representa gràficament per una recta que passa per l'origen de coordenades.

La funció y = mx

Observa els exemples de la pàgina 234 i dibuixa les rectes proposades a l'activitat 1 de la mateixa pàgina.

Podríem dir que tenim dos tipus de rectes, unes amb pendent + i les altres amb pendent - ( negativa ).

Per representar la gràfica d'una funció d'aquest tipus n'hi haurà prou en fer una petita taula de valors que calculi dos punts correctes de la recta.

0	0
4	3

Dibuixa tu mateix d'aquesta manera almenys tres rectes proposades a les activitats de la pàgina 235 del llibre.

Observa també que el pendent de la recta ( valor numèric que ens dona una idea de la inclinació que te la recta ) coincideix sempre amb el valor de m, es a dir, el coeficient que multiplica a la variable independent x.

Hi ha moltes altres situacions on la recta no passa per l'origen de coordenades (0,0), en aquests casos les variables no son directament proporcionals.

L'equació és explícita, la constant ens indica generalment l'altura a l'origen de la recta.

Completa tu mateix les activitats de la pàgina 236 del llibre, corresponen al model comentat a dalt.

El nom de les variables no sempre és , sinó que depèn de les magnituds que representen ( longitud, espai, temps, àrea, etc. )

Equació punt-pendent.

Hi ha una manera sistemàtica de trobar l'equació d'una recta que passa per un punt donat (x0, y0) i de la que coneixem el seu pendent. Ve donada per la fórmula del llibre de la pàgina 237.

Aquesta regla ens permet trobar l'equació de les rectes proposades a les activitats 1,2 del llibre de la pàgina 237.

Vegem la recta d'equació

• Fes tu mateix un dibuix semblant dels altres casos proposats trobant prèviament dos punts de la recta a partir de l'equació explícita de la recta.

• L'activitat 2 de la mateixa pàgina és diferent, a partir del dibuix, intenta determinar el pendent de la recta i almenys les coordenades d'un punt que pertany a la recta.

12. Estadística.

Actualment, una gran quantitat de dades que rebem ens arriba en forma de taules o gràfics estadístics. De vegades convé calcular certs paràmetres que ens ajuden a comprendre d’una manera global aquestes dades.

En aquesta unitat parlarem bàsicament de tres aspectes de la Estadística:

• Taules de dades.

• Gràfics estadístics.

• Càlcul de paràmetres centrals.

A continuació tens diferents gràfics estadístics :

Diagrama de barres.

S’empra normalment en la representació de variables quantitatives discretes ( es a dir, prenen valors aïllats )

A vegades s’empra també per representar variables qualitatives ( població activa, casada, marques comercials, …) es a dir variables no numèriques.

• Fes tu mateix un d’aquests gràfics emprant les dades de la taula de valors que tens a continuació.

Histogrames.

S’empra per distribucions de variable continua ( variables numèriques que poden prendre tots els valors dins un interval )

Per això els rectangles són tan amples com els intervals.

El polígon de freqüències suavitza els escalons de l’histograma.

Diagrama de sectors.

S’empra per tot tipus de variables. Si es representen junts diversos diagrames de sectors relatius a distribucions semblants, és fàcil establir-hi comparacions.

Les Mostres.

Moltes vegades es fa impossible agafar tots els valors de certa variable estadística. Per exemple si a una ciutat hi ha 325.000 votants, per a tenir una idea de les seves opinions polítiques els fem una enquesta a només 1.300 d’ells, elegits a l’atzar.

Cadascun de la mostra representa 325.000: 1.300 = 250 individus de la població. D’aquesta manera podem tenir una idea aproximada del que pensa la població amb cert marge de confiança.

Com veurem en aquest apartat, les mostres poden servir per aconseguir un coneixement prou fiable d’algunes característiques de la població estudiada.

Població és el conjunt de tots els elements que són objecte del nostre estudi.

Mostra és un subconjunt tret de la població. El seu estudi serveix per a deduir característiques de tota la població.

Exemple:

Desitjaríem saber el nombre de peixos de certa espècie que hi ha a un llac.

Pesquem amb xarxa 396 peixos i els marquem fent una mosca a la cola per després tornar-los al llac.

Al cap d’uns dies hi tornem i n’agafem exactament 512 dels quals 27 estan marcats.

Analitzem les dades que tenim a la taula:

	Total individus	Peixos marcats	Proporció
Població	N	396	396/N
Mostra	512	27	27/512

Si suposem que la distribució de peixos marcats a la mostra és la mateixa ( o semblant ) a tota la població deduïm:

, d’on

Podríem deduir per tant que el nombre de peixos està dins l’interval [7000, 8000] amb cert marge de confiança.

Activitats.

• Observa tu mateix altres tipus de gràfics a la pàgina 252 del llibre de Matemàtiques de 3ESO. Contesta tu mateix les qüestions proposades.

• Observa també els gràfics i les definicions de la pàgina 254 del llibre.

• Suposem que tenim una mostra de 30 unitats fabricades d'una empresa d'acer que amiden 28.1 - 27.9 - 27.6 - 28 - 27. 3 - 27.2 - 27 - 27 - 27 - 28.1 - 27.5 - 27.5 - 26.9 - 27 - 27 - 27.3 - 28 - 26.9 - 26.9 - 27.1 - 27.2 - 27.3 - 28.1 - 27.9 - 27.6 - 28 -27.3 - 27.2 - 27 - 27.6

Agrupa tu mateix les dades en quatre intervals per exemple: (26.5 - 27] (27 - 27.5] (27.5 - 28] i (28 - 28.5]

Fes una taula de freqüències i calcula la mitja aritmètica de les dades.

Fes també un gràfic apropiat de la mostra.

• Fes un gràfic apropiat de les dades de l’activitat 1 , apartat a) de la pàgina 259.

Agrupació de dades.

A la pràctica, és freqüent haver de recórrer a una mostra per diversos motius :

• La població és excessivament nombrosa.

• La població és difícil de quantificar ( cas dels peixos al llac )

• El procés de mesurar tota la població és massa car econòmicament.

• Es desitja conèixer ràpidament certes dades i es tardaria massa a consultar tota la població.

De tota manera, cal sempre tenir present que la forma de escollir les mostres pot influir de manera decisiva en els resultats obtinguts.

Una volta escollida la mostra de la variable que es vol estudiar ( moltes vegades amb un 20% de població és suficient ) el millor és agrupar les dades en una taula.

Fixat en els exemples de la pàgina 257 del llibre de Matemàtiques Anaya.

A l'exemple que tens a continuació s'han tirat dos daus de manera aleatòria i s'ha observat la suma obtinguda. Tenim els següents resultats:

11, 10, 7, 4, 6, 7, 7, 4, 11, 4, 4, 7, 5, 8, 2, 11, 9, 10, 10, 4, 5, 7, 7, 4, 7, 8, 8, 4, 8

• Agrupa les dades a una Taula de Freqüències.

• Observa el valor de la suma amb major freqüència ( moda ).

• Fes un Polígon de freqüències amb les dades de la mostra semblant al de baix:

Activitats.

• Fes un diagrama de sectors de les dades de l'apartat b) de l'activitat de la pàgina 257 del llibre de Matemàtiques de 3ESO.

• Fes també un diagrama de barres adequat emprant les dades que tens a la taula de baix: ( Nota: cal agafar una unitat de mesura en milions d'habitants convenient a l'eix vertical del gràfic )

Taules Estadístiques.

N’hi ha molts tipus, aquí veurem l’agrupació de dades amb la seva freqüència i el càlcul de les columnes que ens permet calcular la mitja i la desviació típica de la variable numèrica.

Exemple:

Correspon a l’exercici 15 de la pàgina 211 del llibre Matemàtiques_A.

A un grup de 30 persones del personal de l’Hospital Sant Joan de Deu se li ha pres el nombre de pulsacions per min. I s’han obtingut les dades que hi apareixen.

Ordenem les dades de menor a major i obtenim la taula de freqüències :

xi	fi	Xi·fi	|xi-x0|	|xi-x0|·fi
(60,65]	5	312,5	11,7
(65,70]	5	337,5	6,7
(70,75]	7	507,5	1,7
(75,80]	5	387,5	3,3
(80,85]	4	330	8,3
(85,90]	4	350	13,3
Sumes…	30	2.225

Mitja aritmètica.

Ens dóna el promig de les dades numèriques. Cal calcular altres paràmetres per tenir més informació de la distribució.

= = 74,2 (aprox. a 2 xifres decimals)

Desviació mitja.

Ens dóna una idea global del desviament de les dades respecte la mitja. Ja és un indicatiu de la possible dispersió de les dades.

(pots fer el càlcul amb les dades del exemple)

Pots completar també tu mateix els càlculs de la darrera columna de la taula anterior per ajudar a fer el càlcul.

Desviació típica.

És un paràmetre semblant a l’anterior però ara exagerant una mica les desviacions de la mitja i fent finalment l’arrel quadrada per compensar.

Valors més grans que 0,1 d’aquest paràmetre indiquen ja certa dispersió a les dades numèriques.

• Afegeix a la taula anterior dues columnes que et permeten calcular la desv. Típica. Hauràs de sumar la darrera columna, dividir pel nombre de dades i finalment fer l’arrel quadrada.

Calculadores.

La majoria permeten entrar dades estadístiques en la forma:

· i ens sortirà l’abreviació SD a la pantalla que ens indica que la calculadora està disponible per rebre dades.

Les dades s’entren en la forma:

62,5 (dada) x 5 (freqüència)

67,5 (dada) x 5 (freqüència)

.

.

fins esgotar totes les dades.

Aleshores, la majoria de calculadores ens permeten demanar directament els paràmetres:

Ens torna la mitja aritmètica.

Ens torna la desviació típica que ens dona una idea de la dispersió de la variable estadística respecte la mitja aritmètica.

• Pots completar tu mateix l’exemple que segueix tot ordenant les dades de forma convenient i calculant els paràmetres explicats anteriorment. Si vols pots emprar les tecles de la calculadora abans comentades.

Coeficient de variació.

Per comparar la dispersió de dues poblacions semblants, definim el coeficient de variació com:

CV =

En dividir la desv. típica entre la mitja aritmètica estem relativitzant la dispersió. De vegades els resultats s'expressen en %

Mira tu mateix l'exemple dels pesos de bous i cans de la pàgina 266 del llibre de 3ESO de l'editorial Anaya.

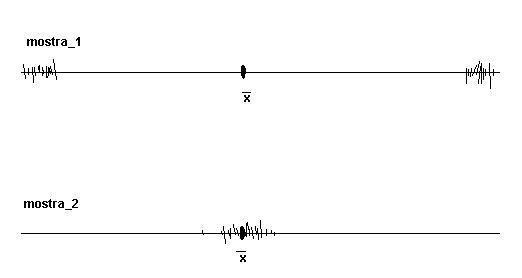
Un altre exemple el tens baix de manera molt més gràfica. Observes les mostres de dues poblacions molt diferents encara que la mitja aritmètica pràcticament coincideix. A la primera mostra, la dispersió és molt més gran i així ho expressaria el coeficient de variació calculat a les dues mostres.

Activitats.

• Fes les activitats 4 i 11 de la pàgina 269 del llibre.

• Fes les activitats 21 i 23 de les pàgines 270 i 271 del llibre de 3ESO de l'editorial Anaya del curs 2002-03.

© Esteve Campins - Maig 2003

http://www2.infotelecom.es/~ecampins/ - Dep. Matemàtiques-Informàtica.