7. Geometria.
Fem primer un petit resum de conceptes bàsics per després parlar de la semblança, d’algunes conseqüències del teorema de Thales i també de resolució de triangles en el pla.
Conceptes.
Figures semblants. Raó de semblança.
Escales.
Teorema de Thales.
Criteris de semblança de triangles.
Teorema del catet i de l’altura.
Procediments.
Reconèixer figures semblants.
Determinar la raó de semblança de dues figures geomètriques.
Utilitzar l’escala per trobar mesures reals.
Identificar triangles semblants i conèixer les seves propietats.
Càlcul de magnituds entre figures semblants.
Elements de Geometria.
Recordem aquí alguns conceptes i procediments bàsics de Geometria. Els angles, els segments, la construcció de triangles, la suma dels angles d’un triangle, les mitjanes, les altures... El teorema de Pitàgores i les seves aplicacions, els polígons en el pla, els polígons regulars.
Angles.
Dues rectes que es tallen al pla formen 4 regions planes que denominem angles. De fet tenim només 2_angles ja que les regions oposades tenen la mateixa “obertura”.

Si dividim un cercle amb 360 parts iguals tenim les unitats sexagesimals, on cadascuna de les parts diem que val 1 º sexagesimal.
A la calculadora observareu l’abreviació DEG a la pantalla.
Les altres abreviacions corresponen a les altres unitats possibles en que mesurem els angles.
GRA. El cercle queda dividit en 400 parts iguals. Cada quadrant té ara 100 º centesimals.
RAD. El cercle es divideix per 2p i ara cada una de les parts no és sencera, correspon a un angle d’un radiant.
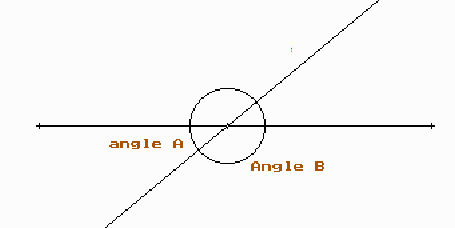
Observa les figures que tens a continuació per determinar la igualtat entre angles. Referència a la pàg. 142 del llibre Matemàtiques 3ESO Anaya.
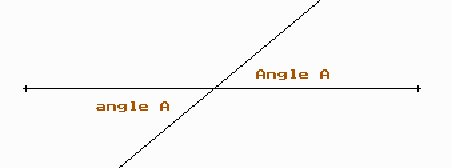
Dos angles oposats pel vèrtex són iguals, tenen la mateixa “obertura”. Si tens a ma un medidor d’angles ( un semicercle graduat ) pots fer l’experiència de comprovar-ho.
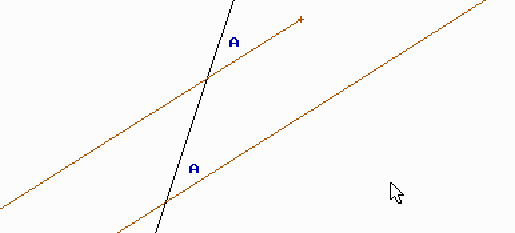
Dues rectes paral·leles determinen angles iguals quan la tallem per una recta r qualsevol.
Els grecs ja tenien una definició d’angle i feien dibuixos en paper de les seves construccions. Avui dia encara que la majoria de plànols es fan amb ordinador és convenient que facis els teus primers dibuixos a ma, ajuda a aclarir els conceptes bàsics de geometria.
La construcció de triangles.
És la més senzilla, hauràs de tenir a ma un regla i compàs. S’explica a la pàg. 143 del llibre Matemàtiques 3ESO Anaya.
Prova tu mateix de fer les següents:
Dibuixa un triangle de costats 7, 5 i 4 cm. respectivament.
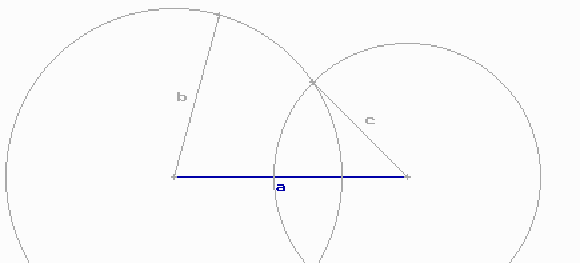
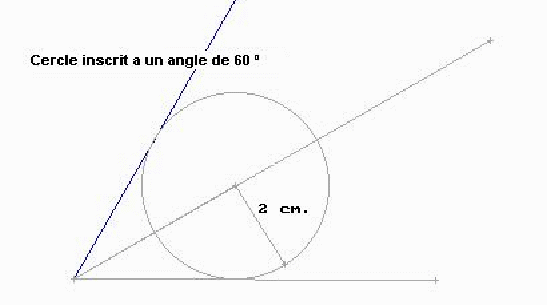
Dibuixa un triangle de costats 7 i 5 cm. que formin un angle de 60 º sexagesimals. Hauràs de tenir a ma el regla i el semicercle graduat. Veuràs un triangle semblant al de la figura de baix.

Dibuixa també un triangle coneixent un costat i dos angles. Per exemple un costat amida 7 cm. i angles 70º i 30º respectivament. Segueix si vols l’esquema de la pàgina 143 del llibre.
Per acabar, fixat que a un triangle qualsevol el costat gran sempre és més petit que la suma dels altres dos costats.
a < b + c
Amb els angles passa exactament el mateix. ( llevat del cas que un dels angles sigui 90º i per tant el triangle és rectangle. )
Els elements d’un triangle.
Si deixem de banda els vèrtex i els costats, tenim altres elements importants com l’altura, la mediatriu d’un costat, l’ortocentre, la bisectriu d’un angle, ...etc.
Agafa per exemple el triangle de costats 7, 4 i 5 cm. respectivament que has dibuixat abans i dibuixa també tots els elements que hi apareixen a la pàgina 144 del llibre 3ESO d’Anaya.
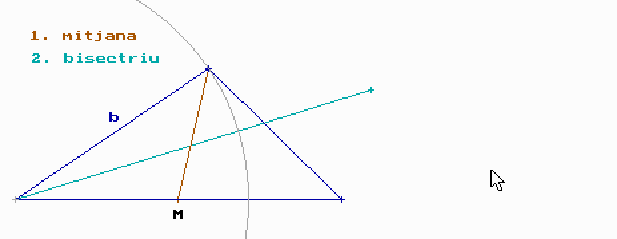
Fes també el famós problema dels tres punts no-alineats. Agafa tres punts qualsevols del pla. Dibuixa amb el compàs un cercle que passi pels tres punts.
Indicació.
El problema és equivalent a trobar el cimcumcentre del triangle que té per vèrtexs aquests tres punts.
Hauràs de tenir a ma el regla i el compàs.
Observa els gràfics de la pàgina 145. Dibuixa també el cercle inscrit al triangle de costats 8, 4 i 7 cm. respectivament. El centre del cercle s’anomena incentre del triangle.
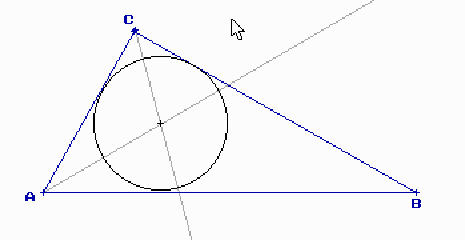
Fes també les activitats proposades a la mateixa pàgina del llibre. Hauràs de tenir a ma el regla numerat i el compàs.
El Teorema de Pitàgores.
És un dels més famosos de les matemàtiques, un dels més antics i també té moltes aplicacions a les construccions geomètriques.
Afirma senzillament que als triangles rectangles és compleix la relació
c2 = a2 + b2
El costat c és la hipotenusa del triangle. ( el costat més gran )
D’altra banda, existeixen molts triangles rectangles de costats sencers, per exemple el de costats 3, 4 i 5 respectivament.
Els alumnes de l’escola pitagòrica ja varen trobar en aquells temps les relacions
![]() ,
,
![]() ,
,
![]()
Que permet trobar infinits triangles rectangles de costats sencers. Completa tu mateix la taula de baix tot variant el valor de n
|
|
|
|
|
3 |
4 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Els polígons en el pla.
Són regions tancades per costats rectes. De fet existeixen polígons amb qualsevol nombre de costats. Un dels fets més pràctics és que qualsevol polígon es pot triangular, podem aplicar així les propietats vistes als triangles, calcular la seva àrea, ...etc.
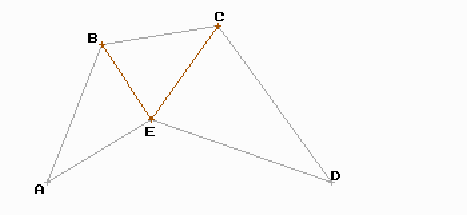
Triangulació d’un polígon del pla.
Observa totes les definicions de les pàgines 148 i 149 del llibre de 3ESO i algunes conseqüències com que els angles d’un quadrilàter sumen 360 º
( el cas més clar, directament observable és el quadrat )
Activitats.
Fes els exercicis 2, 5 i 6 de la pàgina 155 del llibre de 3ESO d’Anaya.
Fes també els 12, 14, 16, 17, 21, 22, 26 i 27 de les pàgines 156 i 157 del llibre de 3ESO d’Anaya.
Fes l’exercici 43 de la pàgina 159
Fes també de la mateixa pàgina els exercicis 49, 50 i 54.
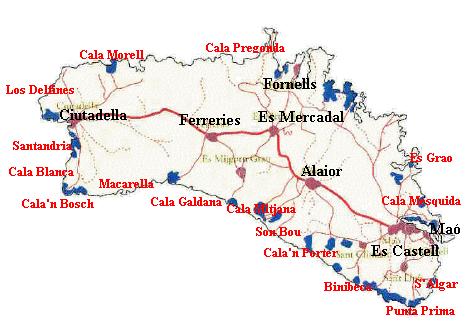
Escales.
El treball amb escales ens permet per exemple determinar les magnituds reals quan tenim un plànol d’un edifici, una carta nàutica o un mapa de carreteres.
Observa els plànols i mapes de les pàgines 182 i 183 del llibre de 3ESO d’Anaya.
Fes les activitats proposades a la pàgina 183.
Figures semblants.
Diem que son semblants aquelles figures que en mantenen la forma i conserven les proporcions. Dit d’una altra manera existeix una raó de semblança que permet trobar les mesures de l’altra figura a partir de les mesures de la figura original.
Exemple:
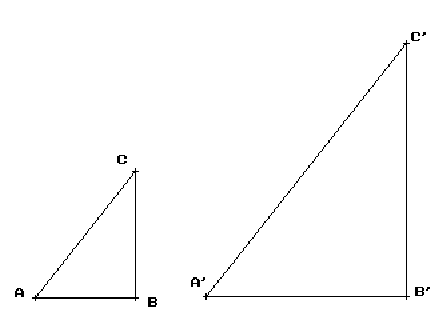
Els triangles de la figura de
baix són semblants. La seva raó de semblança
![]() compleix :
compleix :
![]()
Donades les característiques de les dues figures, també es compleix certa relació amb les seves àrees. Tindríem :
Àrea petit = (1/2)2 · Àrea gran.
Dit d’una altra forma, en quan a les àrees de les figures semblants, la raó de semblança apareix al quadrat.
El teorema de Thales.
Ens diu que rectes paral·leles determinen segments proporcionals sobre 2 rectes qualsevols del pla.
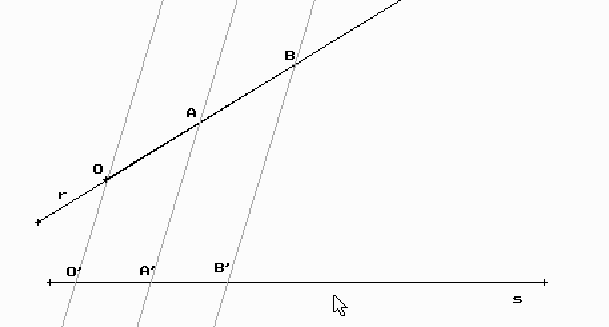
Per exemple, si OB fora 2 vegades OA també es compleix que O’B’ = 2·O’A’
A la pàgina 186 del llibre de 3ESO tens altres variants del teorema.
Fes les activitats proposades a la pàgina 187 del llibre.
Triangles semblants.
Un cas particular són els triangles. Podríem dir que dos triangles són semblants quan:
Tenen els angles iguals.
Tenen els costats proporcionals.
En els triangles rectangles és suficient que un dels angles sigui el mateix o be que dos costats siguin proporcionals.
Algunes aplicacions geomètriques senzilles:
Càlcul d’una distància que no podem mesurar.
Divisió d’un segment en parts iguals.
Activitats:
Les proposades a la pàgina 189 del llibre Anaya Matemàtiques 3ESO.
Dibuixa 2 triangles semblants. Un d’ells de costats 7, 5 i 8. L’altra que tengui totes les mesures ½ de les del primer triangle.
Quina relació hi ha entre les àrees dels dos triangles semblants anteriors ?
Dibuixa un triangle rectangle d’angle agut 35º. Sobre el mateix angle un altre triangle semblant qualsevol. Mesura els costats i comprova que són proporcionals.
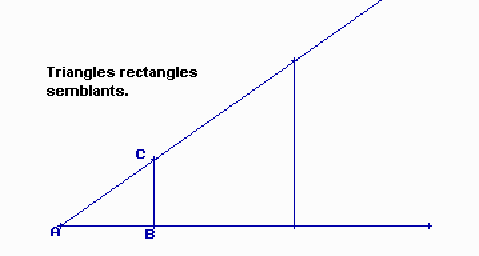
Teorema del catet.
És conseqüència directa dels criteris de semblança i del fet que quan tracem l’alçada sobre la hipotenusa d’un triangle rectangle ens divideix el triangle en dos triangles a la vegada semblants al primer.
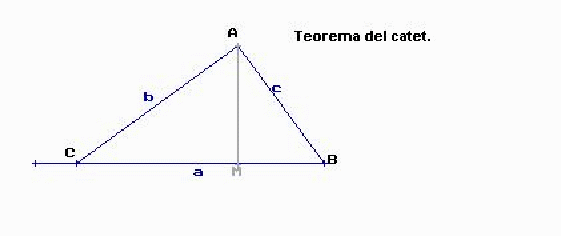
El quadrat d’un catet és igual al producte de la hipotenusa per la projecció del catet sobre ella.
Així per exemple:
b2 = a · longitud de CM
Teorema de l’altura.
També conseqüència dels resultats anteriors, els triangles ACM i AMB són semblants i per tant es compleix:
![]() i d’aquí deduïm multiplicant en creu -->
i d’aquí deduïm multiplicant en creu -->
![]()
![]()
El quadrat de l’altura és igual al producte dels dos segments en que aquesta divideix a la hipotenusa del triangle.
Activitats.
Fes les de la pàgina 191 del llibre de 3ESO d’Anaya.
Llegeix el resum de la pàgina 193, està força bé i resumeix les idees principals d’aquesta unitat.
Fes els exercicis 3, 5, 6, i 7 de la pàgina 194.
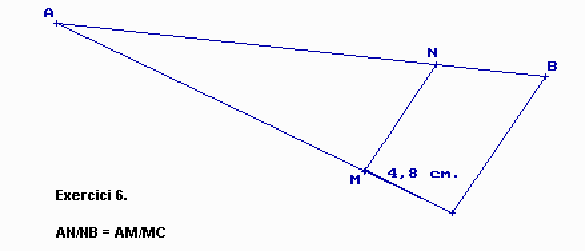
4. Fes també de les pàgines següents, els exercicis 12, 14, 16, 21, 22, 25 i 33. Consulta si tens problemes els exercicis ja fets i el resum de teoria de la pàgina 193.