Estudi de Funcions.

El document és una guia d’activitats per alumnes de Matemàtiques B de 4t ESO. Les sessions es desenvoluparan a l’aula d’Informàtica amb el programa Derive 1.59 que podeu aconseguir a la adreça :

http://www2.infotelecom.es/~ecampins/Programoteca Centre/Derive 1_59.zip

La majoria corresponen al llibre Anaya proposat al Centre, d’altres són propostes opcionals que l’alumne pot seguir, pròpies del Departament de Matemàtiques.

1. Funcions Quadràtiques.

La seva expressió ve donada per y = ax² +bx + c

La seva gràfica és sempre parabòlica, on els coeficients a,b, c tenen diferents efectes a la forma i al desplaçament de la gràfica respecte al origen de coordenades.

• x = -b/2a ens dona sempre la abscissa de l’eix de simetria.

• Els talls amb els eixos es troben fen una de les variables = 0.

• El terme independent c del polinomi sempre desplaça la gràfica cap amunt o cap avall depenent del signe + o – d’aquest coeficient.

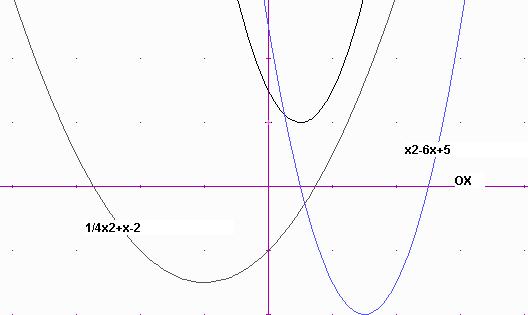2. Gràfiques de les funcions proposades a la pàgina 181.

a)

b)

c)

3. Tall d’una recta amb una paràbola.

És en general la solució ( 2- punts del pla ) d’un sistema d’equacions no - lineal.

Vegem uns exemples.

( Pàg. 183 )

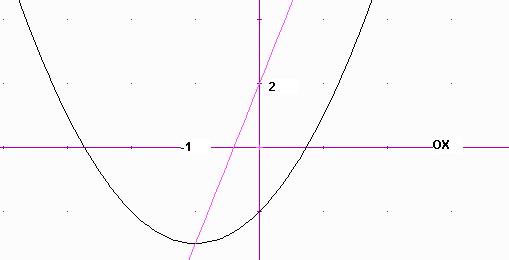
y = x² +2x –2

y = 5x +2

Al gràfic s’observen clarament els 2-punts de tall – solucions del sistema –

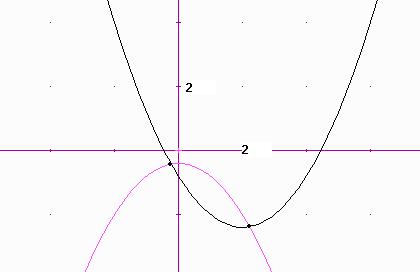• En canvi el tall entre 2-paràboles donarà lògicament 2-punts en general.

Vegem-ho a l’exercici 1 de la pàgina 183.

b) y = -x² –1

y = x² –4x –2

( la segona equació s’ha canviat, així el sistema té solucions i es pot resoldre per substitució de variable )

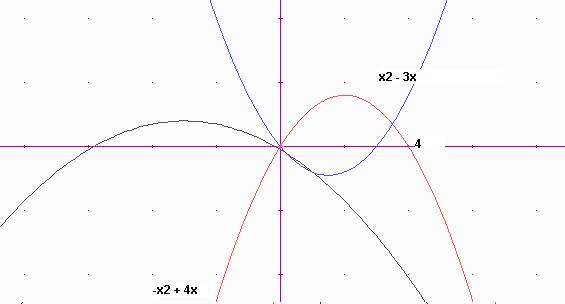
4. Gràfiques de les paràboles proposades a l’exercici 5. (pàgina 187)

• Observeu a les gràfiques que les 3-paràboles tenen un punt comú, l’origen de coordenades (0,0)

• Entreu vosaltres les altres expressions amb el programa Derive i observeu els punts comuns.

5. Expressions aritmètiques de l’exercici 6 (pàgina 187)

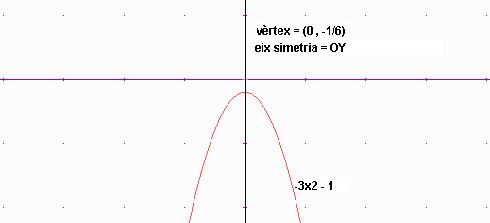• Observareu que només la gràfica d) és una paràbola orientada cap avall que té l’eix de simetria al mateix eix vertical OY.

• Observeu les coordenades del vèrtex a cadascuna de les gràfiques i comproveu les relacions donades a teoria:

vèrtex : x =

y = a·( )² + b·() + c

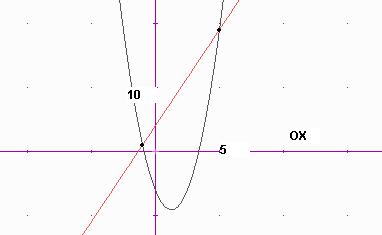6. Resolució gràfica de l’exercici 18. (pàgina 189)

• Observareu la recta i la paràbola de l’apartat

a)

• Vosaltres amb el programa Derive heu de fer l’apartat b) indicant clarament les coordenades del punt de tall.

b)

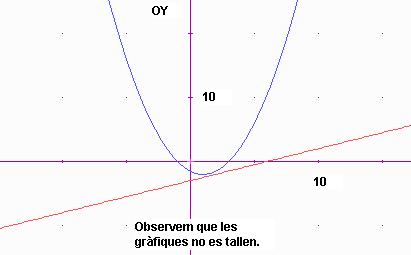7. Comprovació gràfica del fet que els sistemes proposats a l’exercici 20 de la pàg. 189 no tenen solució.

• Vosaltres al gràfic observareu només l’apartat a). Comproveu a mà que el sistema no té solució.

a)

• Feis els gràfics de l’apartat b) i comproveu analíticament que el sistema tampoc té solucions reals.

b)

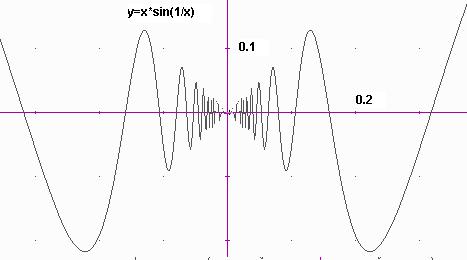
8. Qualsevol relació numèrica entre 2-variables es pot dibuixar amb l'opció “Plot”. Vegem per exemple la gràfica d’una funció que té infinits zeros al voltant de l’origen.

9. L’exercici 40 de la pàgina 191 equival a resoldre una equació que expressa la condició de que el discriminant de la fórmula de Cardano sigui = 0.

D = b² – 4ac = 0

D = (-20)² – 4(4)k = 0

D = 400 – 16k = 0 à k = 400/16 = 25

• L’expressió de la funció ens queda per tant y = 4x² –20x + 25

• Calculeu quan val exactament x al vèrtex de la paràbola i compareu amb el valor observat gràficament.

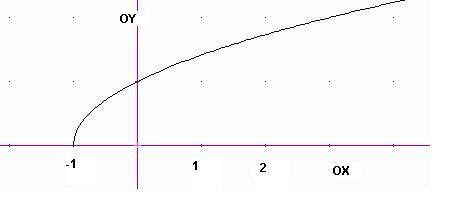
10. Funcions Radicals.

Observareu que la variable x apareix dins el signe radical. A continuació podeu veure alguns exemples.

• Gràfiques de l’exercici 4, 5 de la pàgina 184. Observeu l’efecte de les constants que sumen dins o fora del signe radical.

a) c)

b) d)

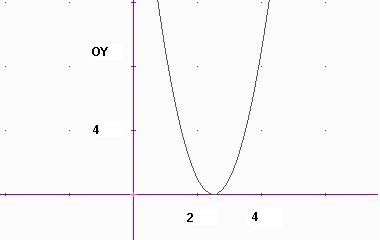
• Observeu també que sempre veiem un tros de gràfica ( als punts on no existeix l’arrel no veiem gràfica ). Per exemple la funció només existeix quan la x és més gran que –1.

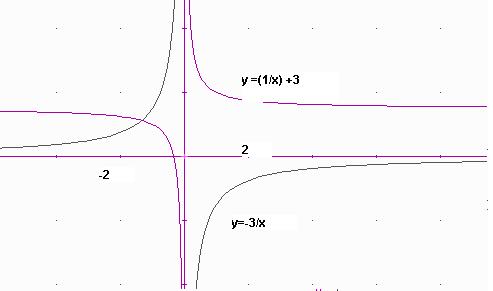
11. Les funcions hiperbòliques.

Les variables x, y són sempre inversament proporcionals ( quan una creix, l’altre decreix proporcionalment). Baix veieu les gràfiques proposades a la pàg. 185 del llibre.

Activitat 1.

Activitat 2.

Activitat 3.

Activitat 4.

• Calculeu a mà el punt d’intersecció de les 2-gràfiques. Haureu de resoldre un sistema no-lineal d’equacions.

• Dibuixeu les altres gràfiques de la pàgina 185.

• Reproduïu amb el programa Derive la gràfica de l’exercici 17. de la pàgina 188

x² –4x + y = 5

2x + y = 14

El sistema té solució ? Quantes solucions ?

• Feis les gràfiques de l’exercici 11. de la pàgina 188

• Resol gràficament un dels sistemes d’equacions de l’exercici 19. de la pàgina 189 del llibre Anaya. Comprova a mà les coordenades dels punts trobats.

a) b)

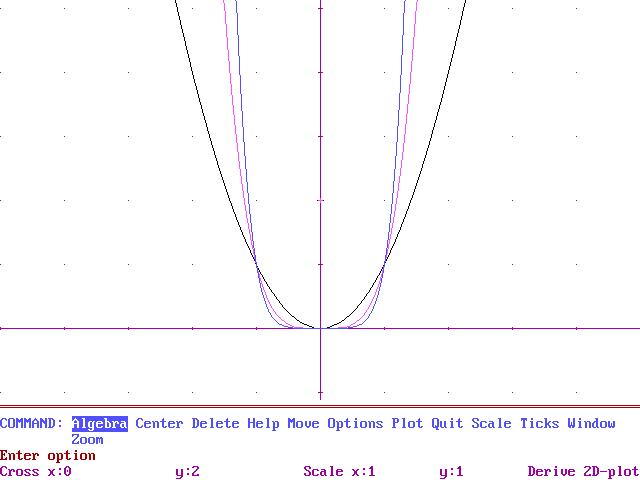12. Els monomis d’exponent

parell.

.

.

etc.

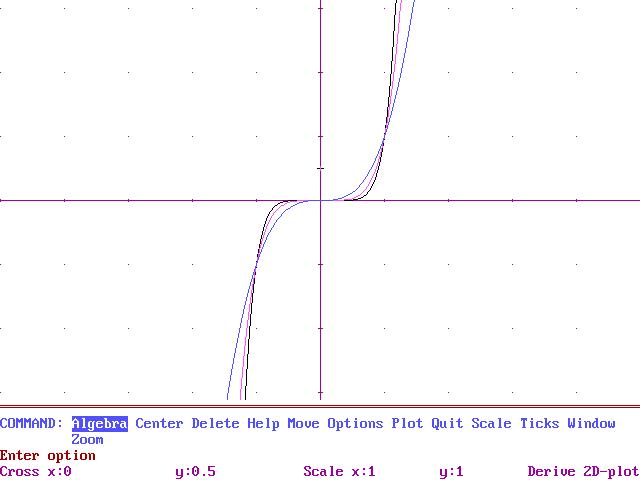
13. Gràfiques de la familia f (x ) = x^2n-1

Observem que totes són simètriques respecte a l'origen de coordenades (0,0)

Matemàticament - f (x ) = f (-x )

[ Valors simètrics de x , tenen imatges amb signe canviat ]

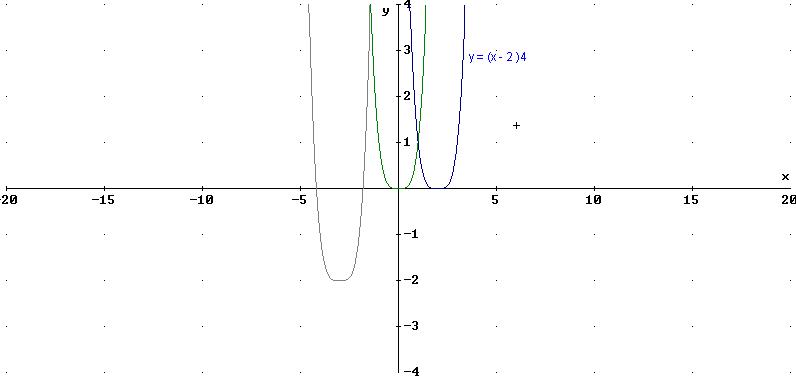
14. Gràfiques de les funcions f (x) = x⁴

g(x) = ( x-2 )⁴

h(x ) = (x+3)⁴ -2

Es produeix en el 1r cas un desplaçament de l'origen cap al punt x=2.

En el 2n cas tenim l'efecte combinat:

- Desplaçament d'origen al punt x=-3

- Desplaçament de tota la gràfica 2-unitats per baix de l'eix OX.

15. Alguns polinomis de 3r grau i de grau-4 [zeros reals = talls observables amb l'eix OX a la gràfica de baix]

f(x) = 3(x-2)(x-1)(x+2) = 3x³ – 3x² –12x +12

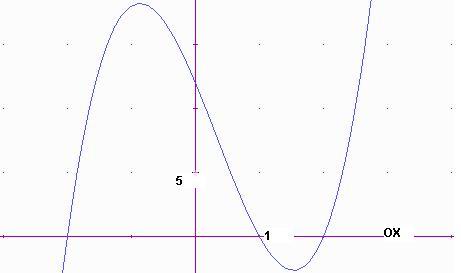
16. Un Polinomi de 3r-grau f(x ) = 3(x-4)(x-1)(x+2)

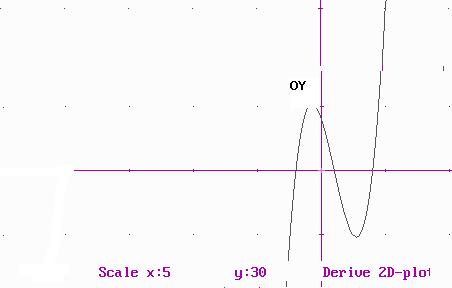
17. Factorització de Polinomis.

f( x ) = 2x² + 3x -2 = (x+2)(2x -1)

Gràfica:

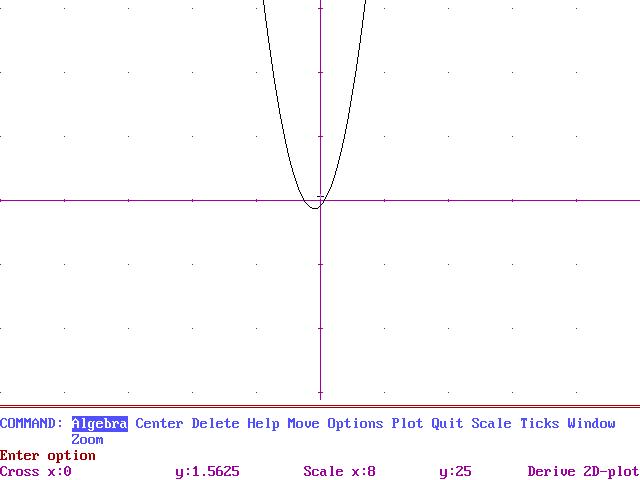
f ( x ) = x⁴ -x³ -7x² + x + 6 = (x-3)(x-1)(x+1)(x+2)

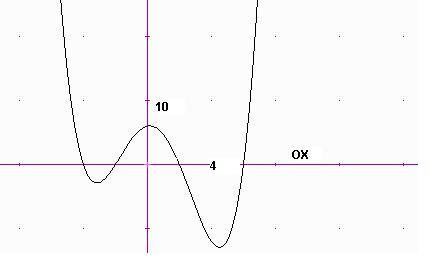
f (x ) = x⁴ -4x³ -3x² +30x -72 = (x-4)(x+3)(x² -3x +6 )

Només té 2-zeros reals 4 i -3

Gràfica:

.

.

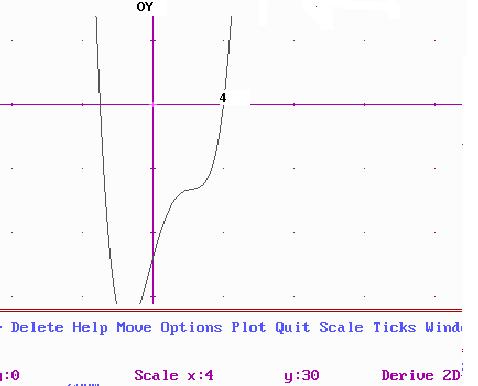
h) f(x) = x³ - 5x² -2x +24 = (x-4)(x-3)(x+2)

i) f(x) = x⁴ -4x³ + x² +6x = x(x-3)(x-2)(x+1)

En aquest darrer cas, tots els zeros són reals ( i sencers ! )

Veurem per tant 4-punts de tall amb l'eix OX à gràfica baix :

18. Resolució de Problemes.

Partim d'una expressió polinòmica que s'anula als punts -3, 2 i 5

f (x ) = K· (x+3)(x-2)(x-5)

Ara imposem que la imatge de zero sigui igual a 3 à

f(0) = K· (0+3)(0-2)(0-5) = K·30 = 3

Deduim així que la constant K = 3/30 = 1/10 = 0,1 (en forma decimal)

19. El polinomi de grau-4 ha de ser del tipus f (x ) = K · (x +5)(x+3)(x-1)(x-3)

A partir d'això deduim el valor de K sabent que quan la x és zero, l'expressió dóna el valor 2,25

f(0)=K·(0+5)(0+3)...etc. = K·45 = 2,25 à

K = 2,25/45 = 0,05 (en forma decimal)

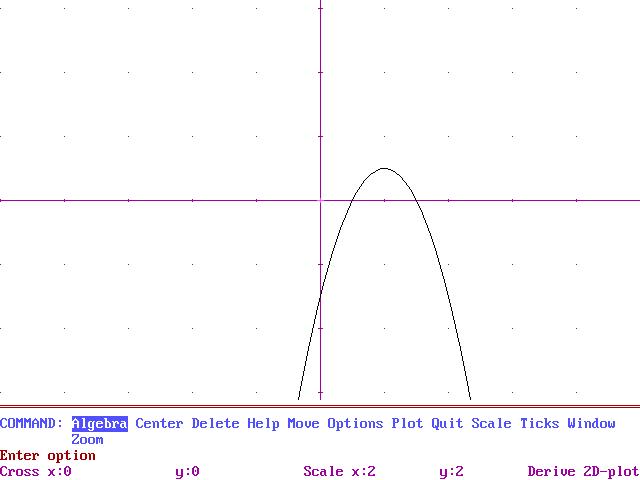
El darrer cas és una paràbola "cap per avall" que té el vèrtex al punt ( 2, 1 ) = (p,q)

Per tant l'expressió és del tipus :

f (x ) = a(x-2)² + 1 on la constant a és negativa.

Si ara observem que passa pel punt ( 0, -3 ) [ Tall amb l'eix OY ]

això ens determinarà la constant à

f (0 ) = a (0-2)2 +1 = 4a +1 = - 3 à a = - 1

Per tant obtenim l'expressió f (x ) = -1·(x-2)² + 1

20. Fraccions Algebraiques.

(Resultats amb el programa Derive 1.59 )

Potenciació.

24. 1,5 · 10⁸ / 4.10⁵ = 375

La distància de la Terra al Sol és unes 375 vegades més gran.

25. Un capital d'un milió ( 1.000.000'- Pts ) col·locat al 12% anual d'interés és un model exponencial com el de baix :

C_f = 1000000·( 1 + 0,12)^t

El milió de pts. al cap de 20 anys ( per t= 20 ) ens donaria un capital final :

C_f = 1000000·( 1 + 0,12)²⁰ = 9.646.293 Pts. ( arrodonim al nombre sencer més pròxim..)

26. El model és semblant a l'anterior on ara V₀ ( Volum inicial de matèria forestal ) = 24000 m3

V_f = V₀ ( 1 + 0,035) ^t

Per tant, només cal substituir V₀ per 24.000 i el temps t per el valor de 20.

27. Les funcions circulars.

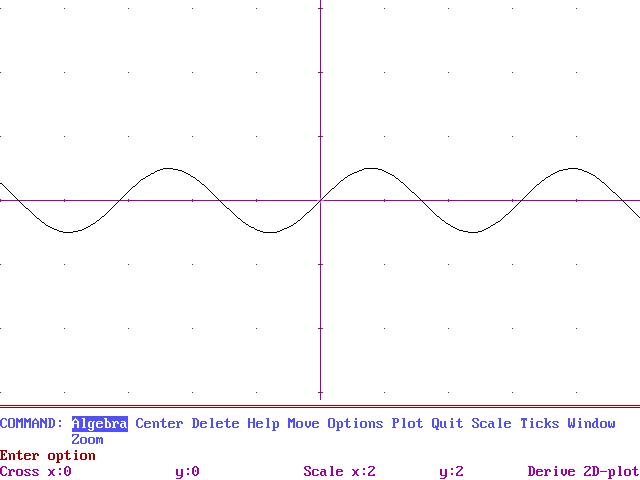
La majoria són periòdiques [ on el període varia segons la modificació que fem a les expressions bàsiques : sin( x ), cos( x ) i tg( x )]

f(x) = sin(x)

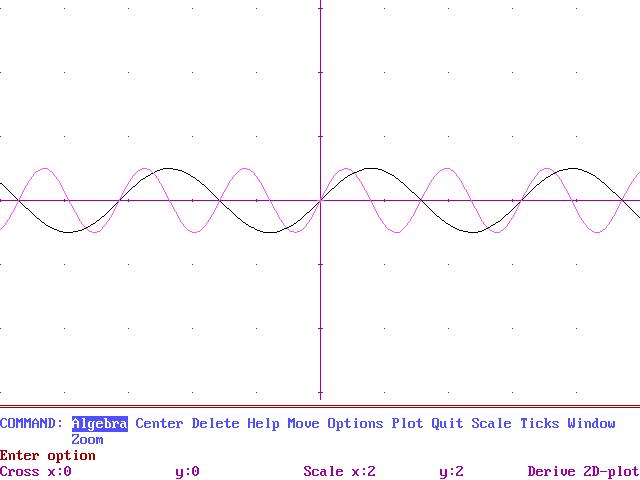
f(x) = sin(2x)

Vegem ara la 2ª gràfica ( posada damunt la gràfica anterior....)

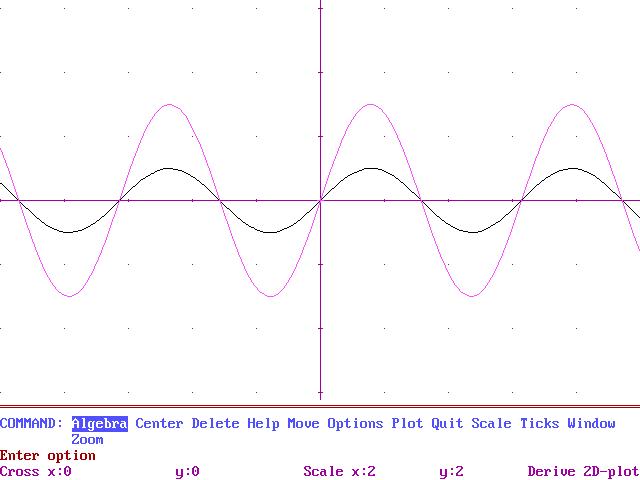
f(x) = 3·sin(x)

La gràfica d'aquesta funció té els mateixos talls i període que la primera f(x)=sin(x).

Ara les imatges són 3-vegades més grans.

28. Polinomis.

Zeros d’un polinomi i descomposició factorial.

Un exemple de la pàgina 59 del llibre Matemàtiques_B consisteix en aplicar la propietat distributiva a un producte de polinomis de primer grau.

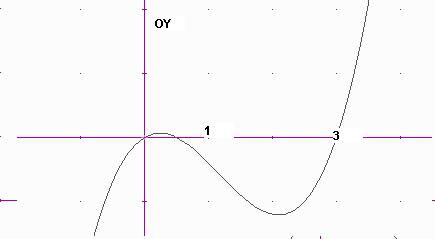
Càlcul numèric dels zeros d'un polinomi.

Quan els zeros són reals, el programa permet aproximar els valors d'aquests zeros amb l'opció soLve (Punts de tall de la gràfica amb l'eix OX)

El programa permet també treballar amb un nombre suficient de xifres decimals de manera

que l'aproximació sigui prou bona.