5. Expressions algebraiques. Equacions

Un dels aspectes que caracteritzen les matemàtiques és el fet d’emprar contínuament equacions. De fet el que interessa més moltes vegades és saber si tenen solució.

 

A la pàgina 105 del llibre de 3r ESO tens un munt d’exemples d’equacions. D’altra banda, no et desanimis, donat que algunes equacions que veurem dins el curs malauradament no tindran solució.

 

Parlarem en aquesta unitat didàctica de tres aspectes bàsics :

 

r       Expressions algebraiques.

r       Equacions i sistemes amb una variable.

r       Resolució de problemes.

 

 

Diem expressió algebraica a una expressió que conté lletres i nombres separats per signes d’operació com +, -, / …

Ex: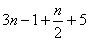 

Les expressions algebraiques permeten descriure situacions, plantejar problemes algebraics i geomètrics, … etc.

 

Altres exemples:

 

1. El doble d’un nombre x..............................................................    2x

2. El doble d’un nombre x, menys 3 unitats....................................... 2x - 3

3. Cinc vegades el resultat de restar 3 unitats al doble d’un nombre.... .. 5·(2x - 3)

 

 

P1.- Si un nombre el representem per  y, escriu les expressions algebraiques que corresponguin amb els enunciats de baix:

 

a) El triple del nombre.

b) El triple del nombre, més cinc unitats.

c) El doble del resultat de sumar cinc unitats al triple del nombre.

d) La meitat de sumar cinc unitats al triple del nombre.

 

 

P2.- La base i l’altura d’un rectangle amiden respectivament: x + 3, x.

Escriu mitjançant una expressió algebraica el seu perímetre i la seva àrea.

x

 
 
 

 

 

 

x+3
 
 

 

 

 


P3. - La base i l'altura|alçària d'un rectangle mesuren 5, x respectivament. Escriu el seu perímetre i la seva àrea.

 

 

P4. - La base i l'altura d'un rectangle mesuren respectivament: x, x-4

Escriu el seu perímetre i la seva àrea

x
 

x - 4
 
 

 

 

 

 

 


P5. - Associa cada un dels enunciats següents amb l'expressió algebraica

que correspongui:

 

 

 

a) El quadrat de la suma de dos nombres és igual a la suma de quadrats més el seu doble producte.

 

x, x - 1, x + 1

 

b) El producto de dos potencias de la misma base es igual a otra potencia que tiene la misma base y exponente la suma de exponentes

 

     x  =  y  =  z

     3      5      8

 

c) Un nombre, el seu anterior i següent.

 

 V = π.r2.h

 

d) Dos nombres parells consecutius

 

 x + (x + 1) + (x + 2) = 33

 

e) La suma de tres enters consecutius és 33.

 

 (a + b)2 = a2 + b2 + 2ab

 

f) Hi ha una diferència de 6 anys entre les edats de dos germans i l'any que ve el germà gran tindrà el doble d'anys que el menor

 

 e = v.t

 

g) Les quantitats aportades per tres socis a una empresa són proporcionals a 3, 5 y 8.

 

 an.am = an + m

 

h) L’espai recorregut per un mòbil es igual a la velocitat per el temps que està en moviment.

 

 x - y = 6

 x + 1 = 2(y + 1)

 

i) El volum d'un cilindre és igual al producte de π pel quadrat del radi de la base i per la seva altura.

 

2n , 2n + 2

 

 

 

P6.- Escriu a la columna de la dreta l'expressió algebraica que correspon al enunciat de la part esquerra :

 

 

a) La meitat d’un múltiple de 3 més cinc unitats.

 

 

 

b) El producte de dues potències de la mateixa base és igual a la potència d’aquesta base elevada a la suma d’exponents.

 

 

 

c) La suma de dos senars consecutius.

 

 

 

d) Un nombre més el seu 10%.

 

 

 

 

SOLUCIONS:

 

P1.-

a) 3y.

b) 3y + 5.

c) 2(3y + 5).

d) 3y + 5

        2

P2.- perímetro = 2(x + 3) + 2x = 4x + 6

       área = (x + 3)x = x2 + 3x.

 

 

P3.- perímetro = 2.5 + 2x = 10 + 2x

       área = 5x.

P4.- perímetro = 2(x - 4) + 2x = 4x - 8

       área = (x - 4)x = x2 - 4x.

 

P5.- a) - 5 . b) - 7 . c) - 1 . d) - 9 . e) - 4 . f )- 8 .

       g) - 2 . h) - 6 . i ) - 3.

 

P6.-

1) (a - b)2 = a2 + b2 - 2ab .  

2) an am  =  an + m .

 

 

 

Expressions  Algebraiques.

Sumes i restes.

Exemples:       

7x2 - x  – x2 + 5x =  6x2 + 4x

x2 - 5x + 7 - (3x2 + 2x - 8) = x2 - 5x + 7 - 3x2 - 2x + 8 = -2x2 - 7x + 15

 

P1.- Agrupa termes del mateix grau:

a) 5x - 3x2 + 4x + x2 =

b) 3x2 - 5x2 + 2x + 3x =

c) 5x3 - 3x2 - x2  +2x =

d) -2 + 7x – ( 10x+ 5 ) =

e) -x3 - 2x2 + 3 ( x3 -3x + 1 ) =

 

Productes.

Exemple:      2x.(3x2 + x - 1) = 6x3 + 2x2 - 2x

 

P2.- Aplica correctament la propietat distributiva i agrupa termes del mateix grau:

a) x2.(x +1) =

b) 2a2(3a2 + 5a - 1) =

c) a(a + b) =

d) 5(3x2 + 7x + 11) =

e) x3 + 2x2 -2x(5x2 + 3x - 8) =

f) 3(x3 - 5x + 7) - (2x3 + 6x2 + 11x + 4) =

g) 2(x - 1) + 3(y + 4) - 2(3x + y) + 9 =

h) 3(x2 + 5) - (x2 + 40) =

Treu factor comú.

Exemples:    

3x2y + 6x3 + x2 = x2(3y + 6x + 1)

xy + x2 + x = x(y + x + 1)

 

 

P3.- Fes el mateix als apartats de baix:

a) 3x2 + 6x =

b) a4 - 3a2 =

c) 6x2 - 3x2 + 3x5 =

d) (x + 1)a + (x + 1)b =

e) -x2 + x - 3x3 =

 

 

SOLUCIONS:

P1.-

a) -2x2+9x  ;                             b) -2x2 + 5x                   c) 5x3-4x2 +2x                                      

P2.- a) x3 + x2                           b) 6a4 + 10a3 -2a2                      c) a2 + ab

d) 15x2 + 35x + 55                   

g) -4x + y + 19                          h) 2x2 - 25

 

P3.-

a) 3x(x + 2)                              b) a2(a2 - 3)                               c) 3x2(2 - 1 + x3)

d) (x + 1)(a + b)                         e) x(-x + 1 + -3x2)                                

                       

 

 

Simplifica Expressions Algebraiques.

Algunes expressions admeten una forma més simple fent operacions com l’exemple que tenim a continuació:

 

Tenim l’expressió algebraica  3(x - 5) + 2x + 3      i posem fraccions equivalents amb el mateix denominador                              4             2

 

 

3(x - 5) + 2.[  2x + 3 ]    = 3(x - 5) + 4x + 6

       4             4                 4               4                      

 

simplifiquem => 

 

 

 

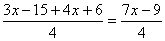
P1.- Fes el mateix amb la suma            3(x - 5) -  x  + 3

                                                                    2         6

 

 

 

 

P2.- El denominador comú és ara 15        x  + x - 2x - 10

 15         5

 

 

 

 

P3.-       x  +  x  +  x  -  3x  - 1

             2      4      8      4     4

 

 

 

 

P4.-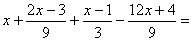     

 

 

 

 

P5.-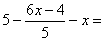 

 

 

 

 

P6.- Escriu una fracció algebraica equivalent amb denominador 6

 

 

 

 

 

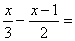
P7.- Ara amb denominador 12 que és el mcm ( 4, 6 )

 

 

 

 

 

 

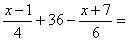
P8.-  

 

 

 

 

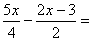
P9.-

 

 

 

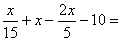
P10.- Altra vegada el mcm ( 3, 5 ) = 15, per tant, el resultat de simplificar serà una fracció algebraica amb denominador 15.

 

 

 

 

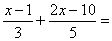
SOLUCIONS:

 

P1.  8x - 27                             

P2.  10x - 150              

P3.  x - 20

P4.  2x - 10                             

P5.  -11x + 29

P6.  -x + 3

 

 

Nota:

Només s’indiquen els numeradors de les fraccions algebraiques corresponents.

 

P7.  x + 415                

P8.   x + 6

P9.  10x - 150

P10. 11x -25

 

 

 

 

 

UN PETIT REPÀS.

P1.- Opera i agrupa termes del mateix grau:

a) 2x2 + 5x - 7 - (x2 - 6x + 1) =

 

 

 

b) 3x - (2x + 8) - (x2 - 3x) =

 

 

 

c) 7 - 2(x2 + 3) + x(x - 3) =

 

 

d) (2x)3 - (3x)2x - 5x2(-3x + 1) =

 

 

 

e) (2x2 - x + 3).(x - 3) =

 

 

f) (-x2 + 3x - 5).(2x - 1) =

 

 

 

P2.- Opera i simplifica agrupant termes del mateix grau:

a) (3x3 - 2x2 + 11).(x2 - 3) =

 

 

b) (x2 - 3x + 1).(6x2 - 6) =

 

 

 

P3.- Multiplica per el mcm per llevar  denominadors i simplifica :

a) 3(x + 2) + 3x + 5 - 5(4x + 1)

         4              2             6

 

 

 

 

 

 

b)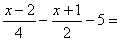

 

 

P4.- Les edats d’un pare i fill són respectivament x, y. Expressa mitjançant una expressió algebraica els apartats de baix:

 

a) Las edades del padre y el hijo hace 6 años.

 

 

b) La suma de las edades del padre y el hijo hace 6 años.

 

 

 

P5.- Expresa mediante una expresión algebraica el área de

la parte rayada de la figura.

 

X
 

10 + X
 
 

 

 

 

 

 

 

 


P6.- El área de un trapecio es la suma de las bases, dividido por dos y multiplicado por la altura.

Expresa el área del trapecio de la figura.

4
 

5+X
 
 

 

 

 

 

 

 

 


P7. - Expressa cada enunciat amb una igualtat entre expressions algebraiques:

a) L'arrel quadrada del producte de dos nombres és igual al producte de les arrels quadrades dels factors.

 

 

b) El quocient de dues potències de la mateixa base és una potència amb la mateixa base, que té com a exponent la diferència dels exponents del dividend i el divisor.

 

 

c) La suma de dos nombres per la seva diferència és igual a la diferència dels quadrats dels nombres

 

 

P8.- Treu factor comú a les expresions de baix

a) x2 + x =                                                       b) 3x + 3 =

c) x2 - 3x =                                                      d) x2 - x =

e) x2 + 2x =

 

Solucions:

P1.- a) x2 + 11x - 8                   

b) -x2 + 4x - 8                          

c) -x2 - 3x + 1

d) 14x3 - 5x2                             

e) 2x3 - 7x2 + 6x - 9                  

f) -2x3 + 7x2 - 13x + 5

 

P2.- a) 3x5 - 2x4 - 9x3 + 5x2 - 33             

b) 6x4 - 18x3 + 18x - 6

 

P3.- a) -13x + 38                      

b) -x - 24

 

P4.- a) x - 6 , y - 6                   

b) x + y - 12

 

P5.- 2x2                                   

 

P6.- 2xy

 

P7.- a) Öx.y = Öx . Öy               

b)  ax  = ax - y                 

    ay

 

c) (x + y).(x - y) = x2 - y2

 

P8.- a) x.(x + 1) ;

b) 3.(x + 1) ;

c) x.(x - 3) ;

d) x.(x - 1) ;

e) x.(x + 2)

 

Polinomis i operacions.

Als polinomis diem grau a l’exponent més alt en que apareix la variable, així:

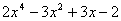 diem que te grau 4

 

Naturalment els polinomis es poden sumar, restar, multiplicar i dividir com la resta d’expressions algebraiques. Fes tu mateix els exemples de les pàgines 76 i 77 del llibre de Matemàtiques_A  4ESO de l’editorial Anaya.

 

Diem valor numèric d’una expressió al resultat que obtenim després de substituir la variable per un dels valors possibles, així:

 

3x2 + 2x + 3  pren el valor 19  quan la variable x=2  ja que 3(2)2 + 2(2) + 3  = 12 + 4 + 3

 

Regla de Ruffini.

En els polinomis, existeix una altra forma de calcular el seu valor numèric que consisteix en emprar només els coeficients del polinomi ordenats per grau i fer sumes i productes a una taula convenient tal com s’explica a la pàgina 90 del llibre de Matemàtiques_A  4ESO de l’editorial Anaya.

 

Fes tu mateix els exemples que hi ha proposats en aquesta pàgina.

 

            3          2          3

 

 

2                      6          16

 


            3          8          19

 

Vegem en aquest cas el valor numèric del polinomi  anterior  3x2 + 2x + 3  obtingut amb la regla de Ruffini quan la variable val x=2.

 

 

 

 

Equacions.

Diem equació a tota expressió aritmètica amb 2-membres separats per un signe =, i que conté una quantitat desconeguda, que anomenem variable.

 

Ex: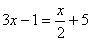 

 

 

Equivalència d'equacions.

Direm que dues equacions són equivalents si tenen

les  mateixes solucions.

 

Exemple:

Les equacions 3x + 9 = 0  i   7x + 21   = 0

són equivalents ja que x = - 3  es la solució per a les dues

 

 

En general:

Dues equacions són equivalents si tenen les mateixes solucions (normalment podem obtenir l'altra equació multiplicant la primera per un nombre real)

 

 

 

Tipus.

Hi ha molts tipus d’equacions, la majoria de les que veurem durant el curs s’ajusten als diferents models que tens a la pàgina 100 del llibre de 3r ESO d’Anaya.

 

Polinòmiques.

Del tipus  3·( x-5 ) – 2x + ( x-3 )/2 = 1.

La majoria tenen solució, moltes vegades tantes com el grau del polinomi que hi apareix a un dels membres.

 

Radicals.

La variable apareix dins el signe Ö , com l’exemple de baix:

 

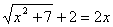
Generalment n’hi ha prou amb aïllar els termes radicals i desprès elevant al quadrat els dos membres per arribar a una equació polinòmica.

  -->   --> 

 

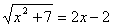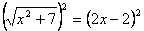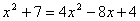
arribem així a una equació polinòmica de 2n grau.

 

 

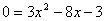
Exercicis.

 

1. Si a un nombre enter qualsevol li diem n, escriu els valors de:

 

a)      El següent de n..........................

b)      L’anterior de n..........................

c)       El següent del doble de n.......................

d)      El triple del següent de n.......................

e)      L’anterior del triple de n.......................

f)       La suma de n amb el seu següent .............

g)      Deu unitats menys que n........................

 

2. Si d’una classe surten 9 nens encara n’hi queden 8. Si surten 7 nenes ni quedarien 11. Quants alumnes té la classe sencera ?

 

 

 

3. El doble d’un nombre més una unitat és 508. Troba el nombre.

 

 

 

 

4. Si sumem el doble de l’edat del Carles amb el triple de la seva edat ens dona 65 anys. Quina edat té en Carles?

 

 

 

 

 

5. Resol les equacions següents:

 

1)     2x – x = 4 

2)     8 + 7x = 3x

3)     -x –x = - 12

4)     2x – 9x = -14

5)     150 – 10x = 5x

6)     x + 2x + 3x = 18

 

 

6. Divideix el nombre 72 en dos sumands de forma que un sigui el doble de l’altre.

 

 

 

 

 

7. Entre dues germanes tenen 653 segells. L’una en té 47 més que l’altra. Quants en tenen cadascuna ?

 

 

 

 

 

 

8. Troba el nombre que sumat amb el seu següent i amb el seu anterior dóna 645.?

 

 

 

 

 

 

 

 

9. Tinc tantes monedes de duro com de 25 ptes. El valor que tenen entre totes és de 330 ptes. Quantes monedes tinc de cada ?

 

 

 

 

 

 

10. Reparteix 1.300 litres entre 3 dipòsits de forma que el primer en tingui el doble que el segon i que el tercer en tingui 100 litres més que el segon.

 

 

 

 

 

 

 

 

11. Les taronges costen a 120 Ptes. El Kg. i les mandarines a 110 ptes./Kg. Un senyor ha comprat quantitats iguals de fruita i ha pagat un total de 1.610 Ptes. Quants Kg. de fruita ha comprat de cada tipus ?

 

 

 

 

12. La Joana té dues capses amb pollets. En una n’hi ha 11 i a l’altra 25. Quants n’ha de passar de la segona capsa a la primera perquè continguin la mateixa quantitat de pollets ?

 

 

 

 

13. El perímetre d’un rectangle és de 420 cm. La llargada fa 14 cm. més que l’amplada. Troba les seves mides.

 

 

14. Resol les equacions amb parèntesis:

 

1) 13 – (6x – 4) = -13

 

 

 

2) –20 + ( 240 – 6x ) = 160

 

 

 

3) –( 11 – 2x ) = 6 + 3x

 

 

 

4) 47 – ( 11 + 5x ) = x

 

 

5) 4x = 7 – (3x – 35 )

 

 

 

 

6) 20x = 18 – ( -7x + 18 )

 

 

 

 

7) 14 – x = - (6 – 3x ) +4

 

 

 

 

Alguns exemples pràctics.

P1.- Mira si 5 es una solución de cada una de las ecuaciones siguientes

a) 7x + 1 = 34   ;                       e) x2 + 7 = 4x + 12

b) x4 - 400 = 225   ;                   f) 2x = 32   ;  

c) 1x = 5   ;                               g) x3 + x2 + x + 1 = 0   ;  

d) x2 + 6x + 5 = 0   ;                  h) 10x + 25 = x3   ;  

i) 3V125 = 2x - 5

 

P2.- Comprova si un dels nombres 4, 7 i 11 és solució de les equacions proposades als apartats de baix:

 

a)  x + 4  +  x - 4  = 4;  

        5           7

 

b) x3 + x2 = 150   ;   

 

c) 3x = 2187   ;  

 

d) xx = 3125   ;

 

 

P3.- Comprova si un dels nombres 1, 2 i 4 és solució de les equacions proposades als apartats de baix:

 

a)    3x   +   4     = 3   ; 

     x + 1    x + 2

 

b) (1 - x)3 - 4x = - 9   ;   

 

 

c)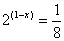

 

 

 

Algunes regles per resoldre equacions de 1r grau.

1r. - Treiem parèntesi, si n'hi ha.

2n. - Treiem denominadors, si n'hi ha.

3r. - Passem a un membre els termes amb x i a l'altre membre els

altres termes

4t. - Simplifiquem els dos membres.

5è. - Aïllem la variable x.

 

 

 

P4.- Resol        x -  x + 2  = 6

                                 3

 

 

 

P5.- Resol        5 -  6x - 4  = x – 3                     P6.- Resol        x  + x =  2x  + 10

                                    5                                                                15             5

 

                                

 

 

15. Expressa en forma algebraica les quantitats següents referides a un nombre qualsevol x.

 

a.          El seu següent...........................................

b.         El seu triple..............................................

c.          La seva meitat...........................................

d.         El seu dècim.............................................

e.         Els dos terços del nombre.............................

f.           El seu quadrat...........................................

g.          El doble del seu següent...............................

h.         Una tercera part del seu anterior....................

i.            La suma d’ell amb la seva meitat....................

 

 

 

16. Si diem 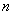 l’edat actual del Pau, escriu la seva edat :

 

j.           Dintre de 20 anys...............................................................

k.          Ara fa 5 anys.....................................................................

l.            Quan en tingui el doble que ara. ............................................

m.       Quan la seva germana Carme, de 16 anys, en tingui 30..................

n.         Quan la Carme tenia 8 anys. .................................................

o.           Quan la Carme tingui doble edat de la que té ara........................

 

 

 

 

17. Resol les equacions. ( Elimina els parèntesis aplicant la propietat distributiva ).

 

 

 

1)     2·(3x – 1 ) = 40 

2)                 33 = 3· (10 – x)

3)                 -4·( x + 6 ) = 60 

 

4)                 4x – 2·(x – 3) = 0

5)     7x + 5·(-3x + 1 ) =13

6)     9x – 6·( 12 – 3x ) = 171


18. Quin és el nombre que si sumes amb el doble del seu següent ens dona 212 com a resultat ?

 

 

 

 

19. A un rectangle de 232 cm. de perímetre la llargada és el triple que l’amplada. Calcula les seves mides.

 

 

 

 

 

 

20. Entre 3 prestatgeries hi ha 129 llibres. A la segona n´hi ha 7 més que a la primera. Si a la tercera n´hi ha el doble que la segona, quants llibres hi ha a cada prestatgeria ?

 

 

 

 

 

 

21. A un pàrking hi ha 28 vehicles entre turismes i motos. Si el total de rodes és de 98, quants vehicles hi ha de cada tipus?

 

 

 

 

 

 

 

22. L’Anna té 13 anys i el seu germà Carles, 9. Quants anys fa que l’edat de l’Anna va ser doble que la del Carles ?

 

 

 

 

 

 

 

23. Sabem que el Felip té 36 anys més que el seu fill Ramon. Si enguany l’edat del Felip és triple de la del seu fill, Quines són les seves edats ?

 

 

 

 

 

 

24. Resol les equacions de baix. (Vigila el signe davant el parèntesis)

 

1)               9 – ( x –4 ) = 7

2)               21 – (x – 5 ) = 17

3)               - (11 – x ) = 6

4)               -7 – (16 +x ) = -27 

5)               x – ( x – 15 ) = -16

6)               –(6–x)+15=15

 

 

 

Equacions amb denominadors.

Primer caldrà multiplicar tota l’equació per un nombre convenient i desprès amb l’equació equivalent seguir de manera habitual. Vegem:

 

3 = 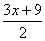  és equivalent a  2·3 = 2·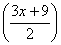,  per tant  6 =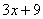

 

25. Resol les equacions llevant primer els denominadors respectius:

 

a)

b)

c)  

d)  

f)  

 

g)

 

h)

 

 

______________________________________________________

 

Exercicis.

 

1. Comenta amb el teu professor els exercicis de la Pàgina 99 del llibre Matemàtiques_A de 4ESO de l’editorial Anaya.

 

 

 

2. Quines de les expressions de baix corresponen al quadrat d’un binomi ?

 

a) x2 –2x + 1

b) 4x2 – 4x + 1

c) 3x2 – 6x + 1

 

 

3. Calcula l’àrea de la figura en funció de la longitud de x

 

 

 

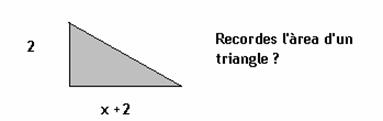
4. Si el càlcul  ( 2a - 1)2  ens dóna 3 sumands després d’agrupar els termes de grau 1. Quants en tindrà el mateix càlcul  ( 2a - 1)3  amb exponent 3 ?

 

Observa que  ( 2a - 1)3 = (2a - 1)· (2a - 1)· (2a - 1)

 

 

 

IDENTITATS NOTABLES.

 

P1.- Donats dos nombres x, i y, expressa cada enunciat amb una igualtat entre expressions algebraiques:

a) El quadrat de la suma de dos nombres és igual a la suma dels quadrats de cada nombre, més el seu doble producte.


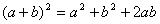
b) El quadrat de la diferència de dos nombres és igual a la suma dels quadrats de cada nombre, menys el seu doble producte.




c) La suma de dos nombres per la seva diferència és igual a la diferència dels quadrats dels nombres.

 

 

 

Per emprar les Identitats Notables.

 

Exemples:

(2a + 7)2 = (2a)2 + 72 + 2.(2a).7 = 4a2 + 49 + 28a

se suele dar ordenado así = 4a2 + 28a + 49

 

(2a - 7)2 = (2a)2 + 72 - 2.(2a).7 = 4a2 + 49 - 28a = 4a2 - 28a + 49

 

(a + 3).(a - 3) = a2 - 9

 

 

P2.- Desenvolupa les expressions :

1) (x + 1)2 =                                                        2) (x + 3)2 =

 

3) (x - 3)2 =                                                         4) (2x - 1)2 =

 

5) (5x + 2)2 =                                                      6) (5x + 2y)2 =

 

7) (x + 1)(x - 1) =                                                8) (x + 3)(x - 3) =

 

9) (2x + 5)(2x - 5) =                                             10) (x2 + 2)(x2 - 2) =

 

 

 

També a la inversa.

Exemples

4x2 + 49 + 28x = (2x)2 + 72 + 2.(2x).7 = (2x + 7)2

 

4x2 + 49 - 28x = (2x)2 + 72 - 2.(2x).7 = (2x - 7)2

 

a2 - 16 = (a + 4).(a - 4)

 

P3.- Expressa en forma de quadrat d'una suma o diferència, o com a producte d'una suma per una diferència:

 

1) x2 + 2x + 1 =                                      2) x2 + 4 + 4x =

 

3) 4x2 + 4x + 1 =                                     4) 4x2 + 9 + 12x =

 

5) x2 - 2x + 1 =                                       6) 4 - 4x + x2 =

 

7) x2  - 6x + 9 =                                       8) x2 - 4 =

 

9) x2 - 1 =                                               10) 4x2 - 9 =

 

11) 16x2 - y2 =                                         12) x2 + 4x + 4=

 

 

SOLUCIONS:

 

P1.- a) (x + y)2 = x2 + y2 + 2xy ;

b) (x - y)2 = x2 + y2 - 2xy ;

c) (x + y).(x - y) = x2 - y2

 

P2.-

1) x2 + 1 + 2x ;

2) x2  + 9 + 6x ;

3) x2  + 9 - 6x ;

4) 4x2  + 1 - 4x ;

5) 25x2 + 4 + 20x ;

6) 25x2 + 4y2 + 20xy ;

7) x2 - 1 ;

8) x2 - 9 ;

9) 4x2 - 25 ;

10) x4 - 4

 

 

 

P3.-

1) (x + 1)2 ;

2) (x + 2)2 ; 3) (2x + 1)2 ; 4) (2x + 3)2 ; 5) (x - 1)2 ;

6) (2 - x)2 ;

7) (x - 3)2 ;

8) (x - 2)(x + 2) ;

9) (x + 1)(x - 1) ;

10) 4x2 - 9 = (2x + 3)(2x - 3) ;

11) (4x + y)(4x - y) ; 12) (x + 2)2

 

 

 

 

Equacions amb denominadors.(repàs)

Recordem una mica les regles per resoldre aquest tipus d'equacions:

 

1r. - Treiem parèntesi, si n'hi ha.

2n. - Treiem denominadors, si n'hi ha.

3r. - Passem a un membre els termes amb x i a l'altre membre els

altres termes

4t. - Simplifiquem els dos membres.

5è. - Aïllem la variable x.

 

 

 

P4.- Resoldre      x - ( x + 2 ) = 6

                                   3

 

 

 

P5.- Resoldre      5 - ( 6x - 4 ) = x - 3

                                   5

 

 

 

P6.- Resoldre      x  + x =  2x  + 10

                         15             5

 

 

 

 

P7.- Resoldre      ( 3x - 5 ) = 1

                        4

 

 

 

P8.- Resoldre      7 -  (x + 4)  = 2

                                      3

 

 

 

P9.- Resoldre      ( 3x - 3)  =  x + 4

                                4              3

 

 

 

P10.- Resoldre  3.(x + 3)  - 2.(2 - 3x) = 8x - 1 - 2.(x + 3)

                               2

 

 

Solucions:

 

P4.- x=10            P5.-  x=4                      P6.- x= 15        P7.- x=3          

P8.- x=11            P9.- x= 5                      P10.- x= -5

 

 

 

Equacions de 2n grau.

Alguns problemes proposats requereixen el plantejament d'una equació polinòmica en una variable, en particular alguns problemes geomètrics senzills que veurem al llarg  del curs.

 

Exemple :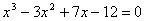 

 

El matemàtic del segle XIX Evarist Galois, famós per la seva contribució a la teoria de Grups intueix que una equació polinòmica té tantes solucions com el seu grau. Arriba a demostrar també que a partir de grau 4, no existeix una fórmula que ens dóna les solucions de l'equació donat que el seu grup associat no és resoluble.



De fet, en aquest curs ens ocuparem només d'aquelles equacions de 2n grau en la seva forma normalitzada, per a les quals existeix la fórmula de Cardano-Vieta que ens dóna directament les solucions:

 

 

 

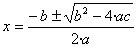
Tingues en compte que quan el discriminant de la fórmula sigui negatiu, no hi haurà solucions donat que l'arrel quadrada dels negatius no és un nombre real calculable.

 

A continuació et proposem algunes equacions normalitzades de 2n grau perquè practiquis amb la fórmula anterior.

 

Exercicis.

 

P1.- Resol tu mateix les equacions :

 

a) x2 - 5x + 6 = 0

 

 

 

 

 

b) 4x2 - 4x + 1 = 0

 

 

 

 

 

 

 

c) x2 +7x + 15 = 0

 

 

 

 

 

 

d) x2 - 6x + 5 = 0

 

 

 

 

e) 6x2 - 5x + 1 = 0

 

 

 

 

f) x2 + 4x + 3 = 0

 

 

 

 

De tota manera, no sempre tindrem la sort que la solució(s) trobades siguin senceres. Quan una equació de 2n grau normalitzada té solucions senceres, existeix una regla molt més fàcil d'aplicar ( coneguda també naturalment per Galois )

 

 

Regla de Vieta.

 

François Viète ( 1540 -1603 ) que per les seves contribucions a l'àlgebra, la trigonometria, l'aritmètica i l'astronomia, és considerat com la figura dominant i central del Renaixement europeu, observa ja en el seu moment que les solucions x1, x2 d'una equació d'aquest tipus compleixen una regla relativament senzilla:

 

 

x1 + x2 = -b

x1. x2  =  c

 

On els termes, b i c són els coeficients de l'equació normalitzada 

 

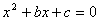
Intenta aplicar teu mateix aquesta regla a algunes equacions dels exercicis anteriors, té l'avantatge que les solucions "es calculen a ull" sense haver d'aplicar la fórmula de Cardano ( que obliga a calcular una arrel ).

 

P1.- Resuelve con esta regla algunos casos anteriores: (compara con las soluciones antes encontradas).

 

a) x2 - 5x + 6 = 0

 

 

d) x2 - 6x + 5 = 0

 

 

f) x2 + 4x + 3 = 0

 

 

De tota manera, en algunes equacions que plantegem com a resultat de l'enunciat de certs problemes, cal fer algunes operacions algebraiques per arribar a la forma :

 

 

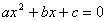
Intenta tu mismo los Exemples que vienen a continuación, en los que tienes que recordar la propiedad distributiva, las reglas de signos vistas, … etc.

 

 

P2.- Resol les equacions següents, arribant primerament a la seva forma normalitzada per aplicar després la fórmula de Cardano o bé la regla de Vieta, segons consideris necessari.:

 

a) (5x - 4).(2x + 3) = 5

10x2 +15x -8x -12 = 5

10x2 + 7x -12 - 5 = 0

10x2 + 7x - 17 = 0   … i ara resols l’equació.

 

b) (x - 5).(x + 2) = 0

 

 

c) x.(3x - 4) = 0

 

 

d) 3.(x - 1)2 = 0

 

 

e) (x + 1)2 - 3x = 3

 

 

 

f) (2x - 3).(2x + 3) - x.(x - 1) = 5

 

 

 

g) (2x + 1)2 = 1 + (x + 1).(x - 1)

 

 

 

Solucions:

P1.- a) 3 y 2   ;  

b) 1/2   ;   c) no tiene solución  ; 

d) 5 y 1   ;   e) 1/2 y 1/3   ;  

f) -1 y -3  ; g) 0'50   ;   h) no tiene solución   ;   i) -3 y -2   ;   j) -1/3  ;   k) no tiene solución.

 

P2.- a) 1 y -1' 70   ;   b) 5 y -2   ;   c) 0 y 4/3 ;  

d) 1   ;   e) 2 y -1   ;   f) 2 y -7/3  ;

g) -1 y -0'67

 

 

 

 

 

Equacions incompletes.

Anomenades així perquè els falta algun coeficient, sigui dit de passada, en aquests casos el mètode de resolució és molt més ràpid que els empleats fins ara. Vegem un parell d'exemples:

 

 

a) 5x2 - 5 = 0

 

En aquests casos, les solucions ( naturalment sempre que l'arrel quadrada sigui possible calcular-la) vénen donades per :

 

 x = ,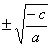

 

 

b) 2x2 - 4x = 0

En aquests casos, les solucions s'obtenen fàcilment factoritzant l'equació i fent zero un dels dos factors possibles:

 

x = 0

x =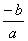

 

 

Nota: Observa que en el primer cas, falta el terme de grau 1, en canvi en el segon, manca el terme que no porta variable. ( o terme independent ) De tota manera, vegem cada un dels casos resolts pas per pas per veure'l més clar:

 

a) 5x2 - 5 = 0

5x2 = 5

x2 = 1

x = 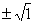 =  1, -1

 

 

 

 

b) 2x2 - 4x = 0

2x·( x - 2 ) = 0 ;  llavors, un dels factors ha d’ésser zero:

 

2x = 0  à   x = 0

 

( x - 2 ) = 0  à  x =2

 

 

 

 

*Resol tu mateix els casos següents aplicant en un o un altre cas aquests mètodes segons convingui.

 

 

Exercicis.

 

P1.- Resol tu mateix per algun dels mètodes anteriors les equacions :

 

a) 5x2 - 5 = 0                               b) 5x2 + 5 = 0

 

 

c) 7x2 + 4 = 18                            d) 3(x2 + 5) = x2 +40

 

 

 

e) 4x2 -9 = 0

 

 

 

 

Les incompletes del tipus ax2 + bx = 0, després de treure factor comú queden de la forma  x(ax + b) = 0

 

Aleshores, las solucions surten de:

 

1) x = 0  

2) i de l'equació de 1r grau ax + b = 0

 

 

 

P2.- Resol factoritzant les següents equacions :

 

a) 2x2 - 6x = 0                                         b) 5x2 + 7x = 0

 

 

 

c) 2x2 - 11x = 0                                       d) x2 - x = 0

 

 

 

e) x2 - 3x = 0

 

 

 

 

 

 

 

6. Sistemes d’Equacions.

Algunes situacions ens obliguen a plantejar un sistema d'equacions ( a utilitzar més d'una equació a causa que apareixen diverses variables ) ja sigui en algunes situacions geomètriques o numèriques que veurem al llarg del curs.

 

De tota manera, veurem els casos més senzills, 2 equacions lineals amb 2 variables, semblants al de l'exemple:

 

x + y = 3

x + 2y = 4

 

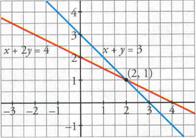
Tots els sistemes lineals d'aquest tipus poden resoldre's pels mètodes clàssics de substitució, reducció o igualació de variables.

 

 

 

Interpretació gràfica.

De fet, resoldre un sistema d'equacions lineals obliga a creuar dues rectes en el pla, cada una de les equacions correspon als punts de coordenades que pertanyen a una recta.

 

 

 

 

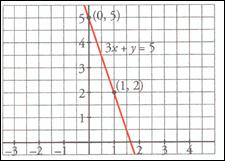
Trobar la solució és equivalent a buscar el punt d'intersecció de les esmentades rectes. ( quan la solució existeix )

 

 

El método de substitución.

Consiste en aislar una variable de una ecuación y substituir dicha expresión en la ecuación restante, que resultará ser de 1r o 2º grado, como los casos tratados anteriormente en este curso.

 

Consulta los pasos seguidos en el primer ejemplo resuelto:

 

 

Exercicis.

P1.- Resoldre per substitució :

a) x = 2y + 5

    3x - 2y = 19  --> 3·(2y + 5) – 2y = 19  -->  6y + 15 -2y =19 -->  4y = 4  --> y = 1

 

De la 1ª ecuación  x = 2y + 5 = 2·(1) + 5 = 7

 

b) y = 5

     4x  +  2y  = 6

      3        5

 

 

 

 

 

 

 

 

c) 5x - 4y = 17

    6x - y = 9

 

 

 

 

 

 

d) 2x + 16 = 2y

    2y - 3x = 16

 

 

 

 

 

Solucions:

a) x = 7, y = 1   ;  

b) x = 3 , y = 5   ;  

c) x = 1 , y = -3   ;   d) x = 0 , y = 8

 

 

 

Mètode de reducció.

S'aconsegueix prescindir d'una variable sumant o restant convenientment les equacions del sistema. Una vegada eliminada una de les variables, l'equació resultant ja és de primer grau, fàcilment resoluble.

 

Fixa't en el primer exemple resolt, després, intenta teu mateix els exercicis que segueixen.

 

Exercicis.

 

P1.- Resoldre per reducció :

a) x = 2y + 5

    3x - 2y = 19

Llevando primero los términos que llevan variable a la izquierda, tenemos el sistema equivalente:

 

x – 2y = 5

3x – 2y = 19

 

Ahora cambiamos de signo todos los términos de la 2ª ecuación, y sumamos:

 

x – 2y = 5

- 3x + 2y = - 19

______________

 

- 2x + 0 = -14  à  2x  =  14 à  x = 14/2 = 7  Aconseguim així fàcilment el valor de la

                                                                      primera variable.

 

 

 

 

b) x – 5 = y

     4x +  2y = 6

 

 

 

 

 

c) 5x - 4y = 17

    6x - y = 9

 

 

 

 

 

d) 2x + 16 = 2y

    2y - 3x = 16

 

 

 

 

 

 

 

El método de igualación.

( llibre pàgina 114 )

Simplemente aislamos la misma variable de las 2 ecuaciones. Igualamos ambas expresiones y determinamos el valor de esta variable.

 

P1.- Resoldre por igualación:

a) x + 2y = 5                   x = - 2y + 5                  Y ahora igualando ambas

                                                                         expresiones,

    x - y = 2                     x = y + 2                      - 2y + 5 = y + 2

                                                                       Ecuación que ya sabemos Resoldre. ..

 

 

 

b) 5 + 3y = 2x

    x + 2y = 9

 

 

 

 

 

c) x =  2y

            5

    x = 4y - 9

 

 

 

 

 

 

 

 

Solucions:

a) x = 3 , y = 1   ;   b) x =  37  , y =  13    ;   c) x = 1 , y =  5

                                          7             7                               2

 

 

________________________________________________________

 

Exercicis.

Vegem alguns exercicis addicionals. Resol teu mateix els sistemes dels següents apartats amb el mètode que prefereixis:

 

a) x = 2y + 5

    3x - 2y = 19

 

 

 

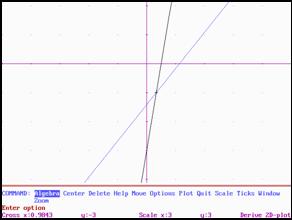
b) 5x - 4y = 17               

    6x - y = 9                   

 

Al gràfic de la dreta veiem clarament el tall de les rectes, solució del sistema.

 

 

 

 

 

 

c) 2x + 16 = 2y

    2y - 3x = 16

 

 

 

 

 

Solucions:

a) x = 7, y = 1   ;  

b) x = 1 , y = -3   ;   c) x = 0 , y = 8

 

 

Problemes d'aplicació.

 

P1. Tres Kg. de peras i 2 Kg. de naranjas cuestan 6'70 Euros. Un Kg. de peras i 5 de naranjas cuestan 7  €. A cuanto está el Kg. de peras? ¿ I el de naranjas ?

 

 

 

 

 

 

 

P2. La suma de las 2 cifras de un número es 5. Si las invertimos en el orden, el número es 9 unidades menor que el primero. De qué número se trata ?

 

 

 

 

 

 

 

 

P3. Resuelve gráficamente el sistema formado por las ecuaciones siguientes:

 

3x + y  = 5

x  +  y  = 1

 

( En una hoja cuadriculada conveniente )

 

 

 

P4. Investiga en los sistemas lineales que tienes abajo los 2 casos que no tienen solución, razonando tu respuesta.

 

 

a) x  + 2y  = 5

    y  - x  = 4

 

 

b) 2x  + y  = 3

    4x  +2y  = 2

 

 

c) x  +  y  = 2

  3x  + 3y = 6

 

 

d) 3x +  y = 2

    x  - y  = -2

 

 

P5. En cierto local hay un cartel anunciando precios:

 

2 Bocadillos +  1 Refresco =  5,35 €

3 Bocadillos + 2 Refrescos = 8,60 €

 

Cuál es el precio del bocadillo ? I el precio del refresco ?